Pinnacle … Часть вторая. Сколько среди игроков профессионалов?

Принято считать, что букмекеры формируют коэффициенты на рынке ставок, используя ту или иную методику определения цен. В первой части этой статьи я попытался составить элементарную модель, чтобы продемонстрировать, как это работает. Моя первая попытка передала суть, но не нюансы формирования коэффициентов. Колебания цен были слишком сильными; модель не могла надлежащим образом адаптироваться к действиям игроков, делающих крупные ставки.

Чтобы компенсировать влияние крупных ставок, в следующей серии испытаний модели я усилил ограничение ставок с 1 до 1/5, 1/10 и, наконец, 1/50 текущего объема. Ниже представлена диаграмма с ограничением ставок 1/50, опять-таки без профессиональных игроков. Исходная ставка на рынке осталась равна 1 единице для A и B, то есть максимально допустимая первоначальная ставка составляет 2/50 = 0,04 единицы. Естественно, этот букмекер разочарует даже самых осмотрительных игроков.

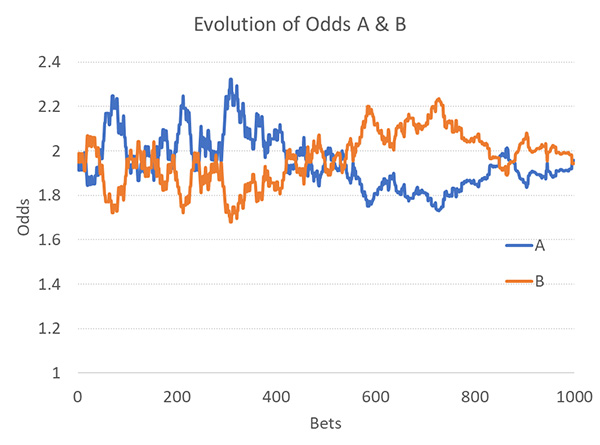
Конечно, такая модель больше напоминает картину настоящего рынка, но колебания цен по-прежнему слишком велики. Мы можем измерить их, используя стандартное отклонение коэффициентов в ходе развития. В этом примере стандартное отклонение составляло 0,116. Это значительно выше, чем наблюдаемые колебания на рынке. Собрав некоторые данные о матчах премьер-лиги, я установил, что стандартное отклонение при изменении средней цены для ставок на общее число голов и азиатский гандикап составляет примерно 0,04.

Мы можем приблизить этот показатель к значению 0,04, добавив в модель профессиональных игроков. Ниже представлены результаты испытания модели, где каждый третий игрок был профессионалом. Разница связана с тем, что размещается меньше крупных ставок. Профессиональные игроки не делают ставки, если цена меньше 2,00, поэтому отсутствует дополнительный объем, который может повлиять на определение цен.

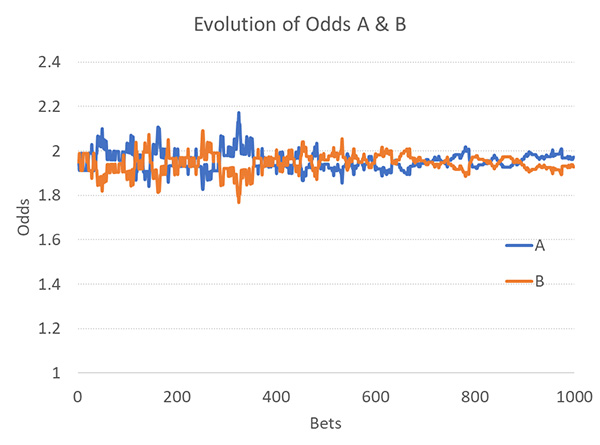
Теперь развитие коэффициентов выглядит более многообещающим (стандартное отклонение составляет 0,041), но мы сталкиваемся с новой проблемой. Испытав эту модель 1000 раз с использованием метода Монте-Карло, я обнаружил, что отклонение между ценами при открытии и закрытии слишком мало. Типичные соотношения цен при открытии и закрытии для ставок на общее число голов и азиатский гандикап на настоящих рынках Pinnacle соответствуют стандартному отклонению около 0,055, но в нашей модели среднее значение за 1000 испытаний составило лишь 0,013.

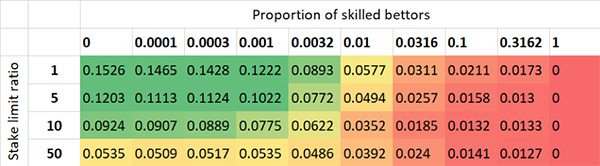
В приведенной ниже таблице показано, как среднее стандартное отклонение соотношения цен при открытии и закрытии за 1000 испытаний модели варьируется в разных тестовых сценариях. Я применил тепловую карту, иллюстрирующую, в каких случаях выходные данные модели значительно выше (зеленый) или ниже (красный) настоящего рыночного показателя 0,055, а в каких близки к нему (желтый). Таким образом, мы можем найти идеально сбалансированные сценарии. Выбранная мною доля профессиональных игроков может показаться немного странной. Используется логарифмическая шкала с эквивалентами 0, 10-4, 10-3,5, 10-3, 10-2,5, 10-2, 10-1,5, 10-1, 10-0,5 и 100 (или 1). Например, показатель 10-2, или 0,01, соответствует значению 1 %.

Стандартное отклонение соотношения цен при открытии и закрытии для разных ограничений ставок и доли профессиональных игроков (исходная ставка на рынке — 1 единица)

Аналогично, во второй таблице показано среднее стандартное отклонение при изменении цен за 1000 испытаний модели. Помните, что в нашем образце с настоящего рынка среднее значение стандартного отклонения составляло примерно 0,04.

Стандартное отклонение при изменении цен для разных ограничений ставок и при разной доле профессиональных игроков (исходная ставка на рынке — 1 единица)

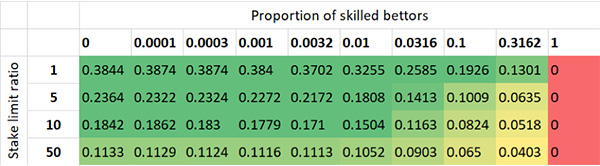
Вы могли заметить, что во всех сценариях испытаний модели отклонение вовсе отсутствует, если все игроки являются профессионалами. В случае данной модели это неудивительно, ведь если каждый игрок «знает», что фактический коэффициент составляет 2,00, то никто из них не поддержит коэффициент 1,95, поэтому рынок не развивается.

Ни в одном из этих сценариев не достигаются идеальные значения стандартного отклонения. Как правило, исходной ставки на рынке, равной 1 единице для A и B, недостаточно, чтобы сократить колебания при изменении цен до реалистичных уровней. Нам следует попробовать увеличить объем исходной ставки. Что касается варьирования соотношений между ценами при открытии и закрытии, вы можете заметить значительное ступенчатое изменение при доле профессиональных игроков около 0,3–1 %. Если профессионалов меньше, варьирование будет избыточным. Если же их больше, оно будет недостаточным. Обратите на это внимание в последующих таблицах.

Изменение исходной ставки на рынке

Несмотря на то что коэффициент ограничения ставок, равный 50, неплохо снижает колебания в изменении цен и соотношении между ценами при открытии и закрытии, такое значение, скорее всего, будет избыточным. В реальной ситуации такое жесткое ограничение серьезно сократит оборот букмекера и доставит неудобства клиентам. Вместо того чтобы повышать это ограничение, давайте изменим размер исходной теоретической ставки на рынке.

В следующих двух таблицах представлены два набора стандартных отклонений для одной и той же доли профессиональных игроков и диапазона значений исходной теоретической ставки. Например, значение 100 указывает, что букмекер установил исходную ставку на рынке, равную 100 теоретическим единицам, для A и B. К каждой паре сценариев применен коэффициент предела ставок, равный 1.

Стандартное отклонение соотношения цен при открытии и закрытии для разных значений исходных ставок на рынке и доли профессиональных игроков (коэффициент предела ставок — 1 единица)

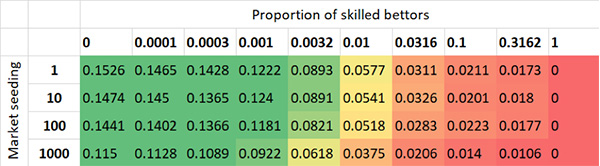
Стандартное отклонение при изменении цен для разных значений исходных ставок на рынке и доли профессиональных игроков (коэффициент предела ставок — 1 единица)

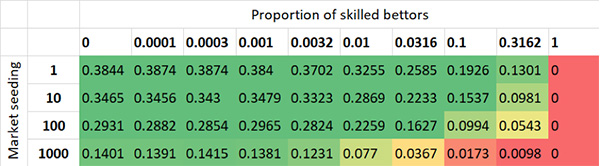
В сценариях с ограничением ставок не существует идеальной пары, где оба стандартных отклонения приближаются к наблюдаемым значениям. Пара сценариев с 1 % профессиональных игроков и исходной ставкой на рынке, равной 1000, является наиболее близкой к идеалу. А теперь рассмотрим развитие в этом примере. Здесь явно что-то не так: внезапные, а иногда и значительные изменения и возвраты сменяются периодами очень ограниченной активности.

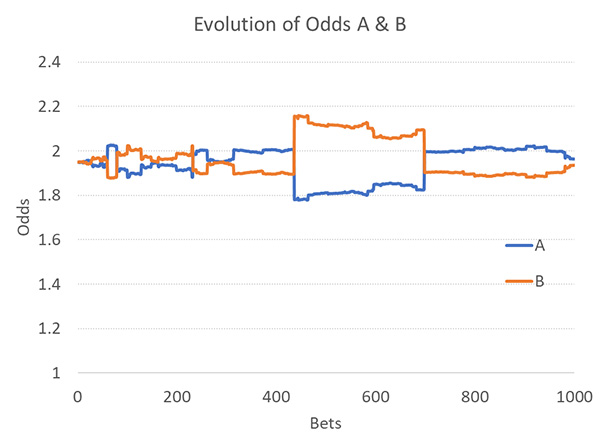
Это вызвано тем, что большие ставки могут оказывать влияние даже при высоком объеме исходных ставок на рынке. Более того, захочет ли вообще букмекер устанавливать на своем рынке исходные ставки такого большого объема? Это серьезно ограничит изменение коэффициентов для небольших ставок, на которые приходится подавляющее большинство активности, как показано на диаграмме.

А что, если мы попробуем совместить определение размера исходных ставок на рынке с их ограничением? Вот один из вариантов развития, где исходная ставка составляет 250, ставки ограничены до 1/25, а профессионалами является 1 % игроков.

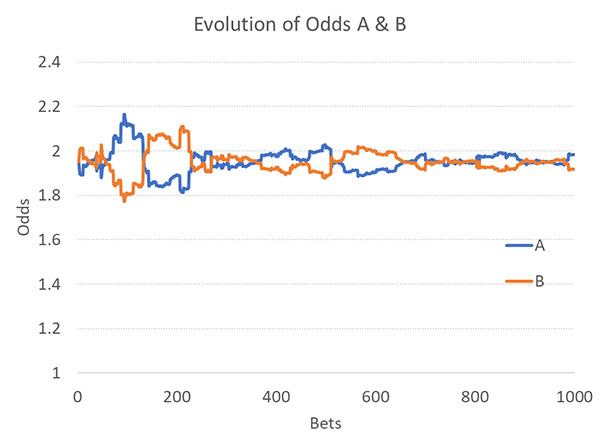
Выглядит намного реалистичнее, не правда ли? Но нам опять не удается найти идеальное совпадение. Стандартное отклонение между открытием и закрытием слишком мало (0,025), в то время как стандартное отклонение изменения коэффициентов слишком высоко (0,064). И по-прежнему наблюдается ряд нереалистичных ступенчатых изменений. Можно ли как-то избавиться от них?

Проблемы с моделью определения цен

До этого момента мы предполагали, что вне зависимости от сценария испытаний модели и квалификации игрока (любитель или профессионал) его действия повлияют на рынок (и коэффициенты) прямо пропорционально его размеру. Но так ли это на самом деле? В случае профессиональных игроков это вполне обосновано. Но как насчет любителей?

Допустим, неопытные игроки отдают непропорциональное предпочтение стороне A, а не B, что наблюдается на рынках ставок «больше-меньше» и гандикапа. Зачем букмекеру обращать на это внимание, если у него есть проработанная модель прогнозирования и возможность избегать необоснованных решений? Почему бы не проигнорировать их действия при пересчете коэффициентов? Допустим, контингент непрофессиональных игроков вдвое чаще делает ставки на A, чем на B. Если не игнорировать некоторые из их действий, может получиться представленная ниже картина. Легкая добыча для профессиональных игроков.

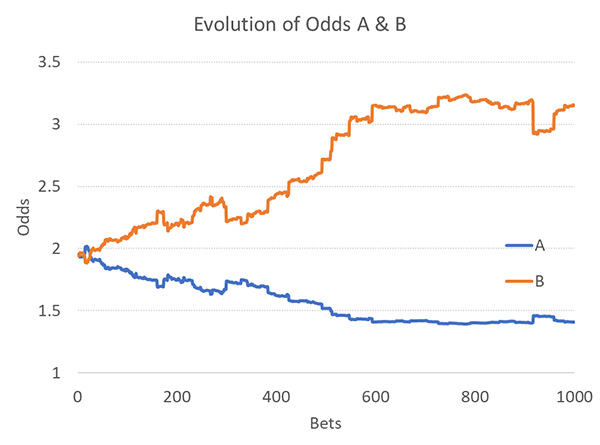
На самом деле, конечно, такими большими отклонениями от «настоящих» вероятностей различных исходов вскоре воспользовались бы профессиональные игроки, а когда стало бы очевидно, что коэффициенты «неправильные», то за ними последовали бы и любители. Клиенты могут не замечать неэффективность рынка только до определенного момента, даже если это относительно неопытные игроки. Как бы то ни было, такая точка зрения ставит под вопрос само толкование поддержания баланса путем определения цен.

Если букмекер проигнорирует (по крайней мере отчасти) действия неопытных игроков, это неизбежно приведет к ситуациям, когда ему придется занять рискованную позицию, где один из исходов матча может привести к значительным убыткам. Понятно, что букмекеры, чья работа не терпит неопределенности, предпочитают избегать таких ситуаций. Но если у них есть возможность анализировать и контролировать эти рискованные позиции, увеличив при этом прибыль, то почему бы и нет?

Игнорирование действий неопытных игроков

В последней подборке сценариев я применил диапазон коэффициентов реакции букмекеров на действия неопытных игроков. Коэффициент 1 означает, что букмекер реагирует на все действия, как в описанных выше сценариях, учитывая все ставки при пересчете шансов. Если задан коэффициент 2, то половина действий учитывается, а другая половина игнорируется. При коэффициенте 64 учитывается только 1/64 действий. В этих сценариях я установил для исходной ставки на рынке значение 100, и задал значение 5 для коэффициента ограничения ставок, чтобы предотвратить чрезмерную реакцию рынка на крупные ставки профессиональных игроков. Ниже представлены тепловые карты стандартного отклонения.

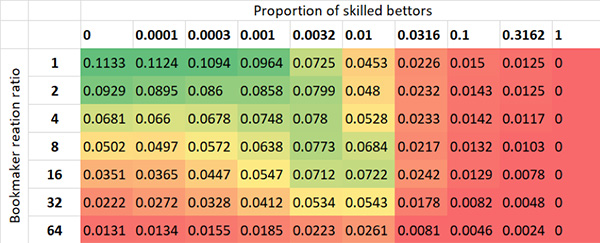
Стандартное отклонение соотношения цен при открытии и закрытии для разных значений коэффициента реакции букмекеров на действия неопытных игроков и доли профессиональных игроков (исходная ставка на рынке — 100 единиц, коэффициент ограничения ставок — 5)

Стандартное отклонение при изменении цен для разных значений коэффициента реакции букмекеров на действия неопытных игроков и доли профессиональных игроков (исходная ставка на рынке — 100 единиц, коэффициент ограничения ставок — 5)

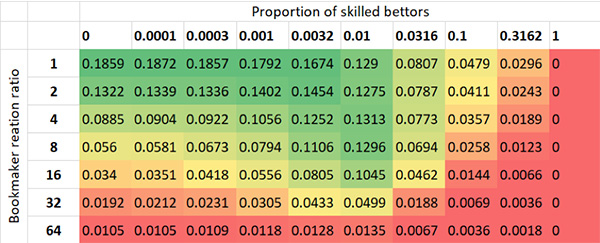В глаза бросаются несколько особенностей. Во-первых, снова можно заметить «стену возможностей» в отношении доли профессиональных игроков, по прошествии которой остается недостаточно вариаций в соотношении между ценами при открытии и закрытии или в ступенчатом развитии рынка. Эта точка находится примерно на 1 %. При большем количестве профессиональных игроков слишком многие отказываются от ставок (это невыгодно). Из-за этого колебания шансов оказываются ниже типичных уровней. Так выглядит типичное изменение шансов, если 5 % игроков являются профессионалами. На мой взгляд, тут слишком «тихо».

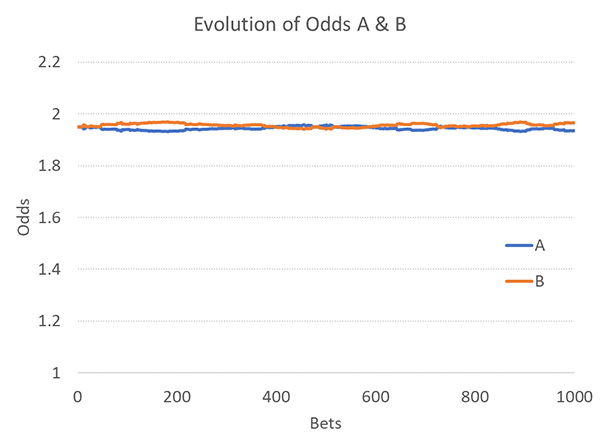
Во-вторых, в сценариях с очень низким или нулевым процентом профессиональных игроков оба показателя по-прежнему слишком сильно варьируются, если только букмекер не применит значительный коэффициент игнорирования действий неопытных игроков. Вот типичная диаграмма для всех неопытных игроков, где букмекер игнорирует только половину их действий. Тут слишком «шумно» и беспорядочно.

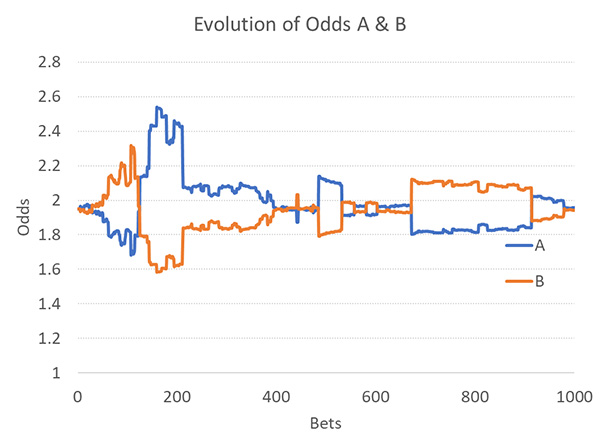
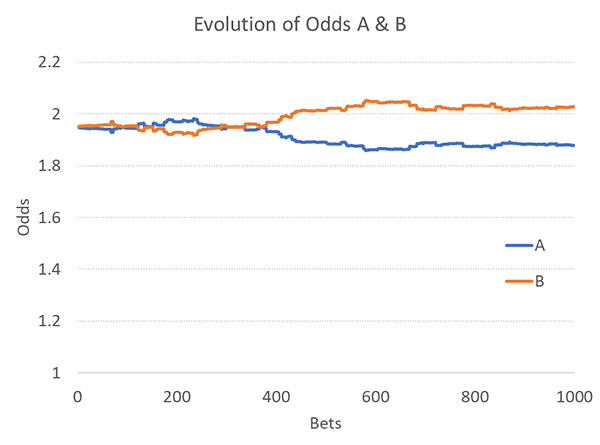
Наконец, у нас есть заветная зона, где доля профессиональных игроков относительно мала (возможно, от 0,1 до 1 %), а коэффициент реакции букмекера относительно высок (32). Если коэффициент будет выше, шансы снова перестанут колебаться. Это неудивительно. Если бы букмекеры игнорировали все действия, то рынки без профессиональных игроков не менялись бы совсем. Так выглядит типичное изменение шансов для этого сценария, если 0,3 % игроков являются профессионалами.

Что мы узнали об определении цен?

Мы составили модель определения цен, призванную воспроизвести настоящее развитие двусторонних рынков, например для ставок на разброс очков или азиатский гандикап либо ставок «больше-меньше». Мы обнаружили, что букмекеру необходимо установить на своем рынке теоретические исходные ставки, чтобы инициировать изменение коэффициентов в соответствии с действиями игроков, а также следует применить некоторые ограничения на эти действия. Наконец, при пересчете этих коэффициентов имеет смысл игнорировать многие действия неопытных игроков.

Я считаю, что эти параметры модели представляют реалистичное поведение букмекера. Мы знаем, что букмекеры применяют ограничения ставок, влияние которых более значительно на ранних этапах развития рынка, когда общий объем ставок меньше. Кроме того, при запуске рынка также есть смысл в установлении теоретической исходной ставки. Без этого ранние цены будут колебаться, сильно отклоняясь от «настоящих».

И наконец, ни для кого не секрет, что профессиональные игроки, располагающие важной информацией для рынка, будут оказывать на него куда большее влияние, чем те, кто делает ставки, полагаясь на интуицию. Компания Pinnacle открыто заявляет, что ее наиболее успешные клиенты помогают повышать точность коэффициентов. Некоторые из них даже могут получить такую возможность еще до того, как рынок откроется для широкой публики. Это, в некотором смысле, можно считать установлением исходных ставок на рынке.

По-прежнему остается вопрос: сколько среди игроков профессионалов? Испытав модель в ряде сценариев с варьированием этих трех параметров, я пришел к выводам, подтверждающим гипотезу, что вероятная доля победителей (как я назвал их в начале первой части этой статьи) среди игроков очень мала и находится в диапазоне 0,1–1 %.

Как я уже предупреждал в начале цикла этих статей, модель определения цен и изменения шансов основана в первую очередь на моем мыслительном процессе. В нем может быть много противоречий и ошибок. Кроме того, я не учел возможность того, что букмекер также проигнорирует некоторые действия профессиональных игроков, посчитав, что его квалификация выше, чем у некоторых из этих клиентов.

Однако я проводил испытания в условиях, являющихся типичными для настоящих рынков, где предвзятые игроки делают ставки на A чаще, чем на B. Используя соотношение 2:1 и надлежащим образом взвесив внимание букмекера к неопытным игрокам, делающим ставки на A и B, мне удалось воссоздать показатели и диаграммы, очень близкие к приведенным выше.

Наверное, наиболее значимой слабостью модели является фиксированное количество итераций — 1000 (и, как правило, около 500 ставок). На реальных рынках эти показатели могут быть намного ниже или намного выше, что может повлиять на варьирование соотношения между ценами при открытии и закрытии.

Иными словами, практически вся моя работа основана на предположениях. По крайней мере, эта модель должна была показать, как букмекеры могут развивать свои рынки ставок в процессе определения цен, в ходе которого они обращают больше внимания на малую долю профессиональных игроков, чем на большинство любителей. Чтобы войти в число первых, вам придется усердно трудиться. Для начала вы можете прочесть остальные учебные статьи от Pinnacle.

JOSEPH BUCHDAHL