Pinnacle … Часть первая. Сколько среди игроков профессионалов?

Возвращаясь к классическому вопросу

Вопрос, который интересовал меня долгое время, — сколько людей действительно выигрывают на ставках. Когда я впервые задумался об этом, я поискал и обнаружил, что 97 % игроков проигрывают. Если быть точным, то эта цифра немного варьируется: иногда это может быть 95 %, а иногда — 99 %. Но что эти цифры означают на самом деле? И что более важно, на сколько они достоверны?

Давайте для начала попробуем ответить на вопрос полегче: «А что такое выигрыш?» Естественно, каждый может сделать ставку и выиграть благодаря удаче. Фактически довольно немало людей выигрывают на ставках много раз подряд только благодаря везению. Почти четверть игроков, делающих ставки на разницу в счёте или с азиатским гандикапом и с ожидаемой стандартной маржой Pinnacle, могут быть в плюсе и после 1000 ставок. Один из ста остается с выгодой даже после 10 000 ставок. А кому-то везет всю жизнь.

Но не это мы имеем ввиду, когда говорим про выигрыш. В конечном итоге большинство игроков удача покидает. Здесь работает закон больших чисел. Для нас более интересны те игроки, которые могут выиграть благодаря опыту, а не просто везению. Такие игроки нашли способ генерировать то, что называется ожидаемой выгодой. Букмекеры ждут от таких игроков попадания в плюс даже после того, как они в равной мере испытают и удачу, и невезение. Сколько же игроков действительно удерживают в своих руках ожидаемую выгоду?

Насколько мне известно, опубликованных результатов исследований на эту тему нет. Если вам, наоборот, что-то об этом известно, сообщите мне об этом. Ранее я уже пытался найти ответ на этот вопрос, составляя график распределения результативности размещенных ставок. Но поскольку такой график выглядит почти так же, как случайное распределение результативности, я пришел к выводу, что действительно не может быть очень много опытных игроков.

В этой статье я попытался взглянуть на это снова с другой стороны баррикад, с точки зрения букмекеров, и более конкретно показать, как они развивают свои рынки. Здесь я должен подчеркнуть, что то, что изложено в паре этих статей, во многом является моим мысленным экспериментом, полным вероятных оговорок, ошибок и пробелов, и никоим образом не претендует на презентацию того, как Pinnacle управляет развитием своих рынков.

Поскольку ни один букмекер не скажет нам, как он это делает, мы должны работать в обратном направлении. Изучить, как на самом деле изменяются коэффициенты, и посмотреть, сможем ли мы построить модель, изменяя ее параметры, пока не воспроизведем реальность. Хотя я бы никогда не стал поддерживать подобный вид анализа данных при разработке методологии ставок, но для поставленной задачи этого будет достаточно.

Уравновешивание потоков ставок и определение цены

Загляните в Twitter или на любой популярный игорный форум, и вы, вероятно, наткнетесь на различные обсуждения того, как букмекеры координируют свои линии (коэффициенты). Стандартно считается, что, разместив по своему мнению наиболее точные цифры, они затем пытаются уравновесить поток ставок, чтобы гарантировать себе получение прибыли независимо от результата.

Когда с одной стороны наблюдается больше действий и ставок, чем с другой, букмекер сдвинет (урежет) коэффициенты с активной стороны, чтобы стимулировать больше действий и ставок на другой стороне. Если игроки клюнут на приманку, он может вернуть исходные коэффициенты, а если нет, то может понизить коэффициенты еще больше.

Таким образом, корреляция рынка букмекером в период до начала матча является в своем роде определением цены. На финансовых рынках это называется определением цены актива на рынке посредством взаимодействия покупателей и продавцов. Аналогичная модель используется и спортивным букмекером; мы просто заменяем цену актива коэффициентами, а взаимодействие покупателей и продавцов заменяем взаимодействием ставящих на команду А и ставящих на команду Б.

Таким образом, если на обе команды А и Б поставили по 100 долларов, букмекерская контора установит честные коэффициенты 2,00 (и 1,95 с учетом маржи). Предположим, что на команду А ставят еще 10 долларов. Относительный баланс теперь составляет 110 долларов против 100 долларов. На основе такой информации букмекер может сделать вывод, что реальные коэффициенты на команду А теперь равны (100/110) +1 (или 1,909) и (110/100) +1 (или 2,10) на команду Б. После добавления маржи это будет 1,86 и 2,05 соответственно. С каждым новым шагом букмекер будет обновлять свои коэффициенты по методологии Байеса.

Одна из проблем с такой моделью связана с началом развития рыночной ситуации. Понятно, что при открытии рынка объем ставок отсутствует. Вы должны выбрать число, неравное нулю, иначе вы не сможете запустить модель. Но какое выбрать? Чем меньше число по отношению к начальному действию, тем больше корреляция стартовых коэффициентов.

Предположим, что в этом примере мы начали с теоретической «затравки» в 10 долл. на А и 10 долл. на Б. Ставка в 10 долл. на А изменит коэффициенты на 1,46 (и на 2,93 для Б соответственно). Такой резкий ход явно был бы нежелателен, поскольку слишком отличался бы от первоначальных оценок модели и побудил бы более опытных игроков воспользоваться ситуацией, сделав крупные ставки.

Очевидно, что букмекер должен применять некоторую теоретическую затравку. Каков будет ее размер, зависит от ставок клиентов.

Модель для развития рынка

Чтобы воспроизвести определение цены букмекером, я построил модель в формате Excel. Модель состояла из вымышленного рынка с командами A и Б, которые, по мнению букмекера, имели равные шансы на победу (честные коэффициенты 2,00). Применялась маржа в 2,5 % (коэффициенты букмекера 1,95). Коэффициенты затем изменялись в серии из 1000 итераций. На каждой итерации у игрока была возможность поставить на А либо на Б или проигнорировать текущую цену.

Если игрок игнорировал цены как на А, так и на Б (полагая, что ни одна из них не принесет выгоды), цены оставались неизменными. Если он делал ставку на А или Б, коэффициенты обновлялись в соответствии с принципами определения цены, описанными выше.

Предполагалось, что предпочтения игроков в ставках соответствовали функции степенного закона, пытаясь воспроизвести вероятный сценарий реального мира. Получается, что когда большинство игроков предпочитали ставить от 1 до 5 единиц, некоторые хотели поставить более 10 единиц, отдельные игроки — более 100, а один или два надеялись выиграть, поставив более 1000 единиц.

Игроки относились либо к профессионалам, либо к неопытным. Предполагалось, что профи знают, что честная цена на А или Б — 2,00. Следовательно, они бы делали ставки только тогда, когда коэффициенты были выше. Предполагалось, что неопытные игроки просто будут следовать за толпой. То есть, на любом этапе развития рынка на них влияли установленные в данное время цены. Если допустить, что якорение, новизна и эвристика доступности обычно влияют на людей, когда их просят принять решения о сомнительном факте, это может быть обоснованным предположением.

Чтобы предоставить им немного свободы, предполагалось, что представление неопытного игрока о реальных коэффициентах будет варьироваться в соответствии с обычным случайным распределением текущих цен. Например, если текущая цена на A была 1,95 и 2,00 без маржи, некоторые могут считать, что реальная цена составляет 1,99, 1,98, 1,97 (или 2,01, 2,02, 2,03) и т. д. Часть игроков будет полагать, что реальная цена будет ниже 1,95, и, следовательно, опубликованная цена 1,95 будет выгодной.

Всегда будут неопытные игроки, которые будут верить, что одна из существующих цен на А или Б является выгодной; в моей модели они будут ставить на установленные ставки. Конечно, не будь этой изменчивой неуместной сверхуверенности, то никаких ставок на рациональном рынке не было бы. Как правило, с уровнем свободы, который я применял к неопытным игрокам, около половины из них могли найти что-то, на что можно сделать ставку в типичной серии из 1000 итераций.

В этой модели сделано еще два предположения. Во-первых, опытные игроки делали самые большие ставки. Хотя это может не совсем точно отражать реальный мир, уместно предположить, что те игроки, которые доказали свою способность удерживать ожидаемую выгоду, с большей вероятностью пойдут на больший риск, особенно потому что они могут делать это, используя капитал, заработанный на предыдущих успешных ставках. Во-вторых, для моего первоначального исследования ставка игрока была ограничена общим объемом ранее сделанных ставок.

Например, если игрок хотел поставить 50 единиц, но на текущий момент было поставлено только 30 (включая затравку), применялось ограничение в 30 единиц. При таком сценарии, с развитием рынка и накоплением количества действий, игроки, которые играют по-крупному, будут делать все возможные ставки. Такая ситуация показательна для рынка Pinnacle, в котором реальные ограничения ставок увеличиваются с ростом объема торгов.

Приведенные ниже временные ряды показывают, как изменялись коэффициенты на А и Б при условии, что затравка составляла всего 1 единицу для каждой команды и опытные игроки не участвовали. Очевидно, что некоторые колебания коэффициентов, особенно в начале развития рынка, слишком велики, чтобы быть реальными показателями действующего рынка. Любая крупная ставка существенно влияет на расчет коэффициентов на основе принципов определения цены, описанных выше. Подобные изменения коэффициентов наблюдались даже на тех рынках, где участвовали опытные игроки. Очевидно, что проблема заключается либо в величине теоретической затравки, либо в размере ограничения ставки.

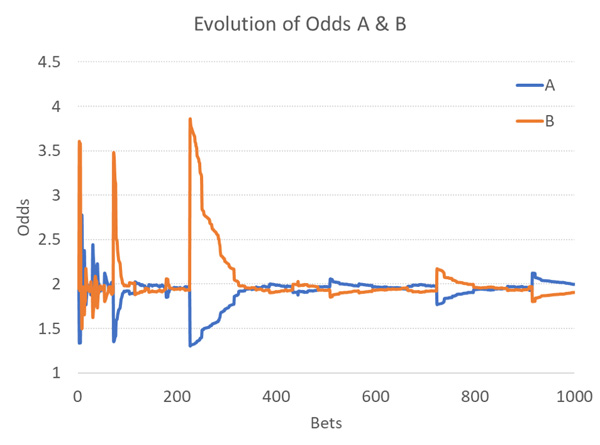
Как мы будем решать подобные проблемы и какое соотношение профессиональных и неопытных игроков будут выдавать такие типичные сценарии модели, рассмотрим во второй части этой статьи.

JOSEPH BUCHDAHL