Pinnacle … Насколько длинной может быть череда неудач в размещении ставок?

Всегда приятно получать выигрыш по ставке. Но проигрыш приносит отрицательные эмоции, которые, по мнению психологов, оказывают воздействие в два раза сильнее, чем ощущение удовольствия при выигрыше. Зачастую ответной реакцией игроков на проигрыш (в особенности на череду проигрышей) становится безответственное поведение: пытаясь отыграться, проигравшие начинают размещать ставки чаще или в более крупных размерах.

Даже компетентные игроки, чьи ставки обладают положительным математическим ожиданием, в случае столкновения с чередой неудач могут совершенно иррационально поставить под сомнение эффективность своей системы размещения ставок. Куда проще начать испытывать неуверенность в себе после 10 проигранных ставок подряд, чем после 10 выигрышных, даже если с точки зрения статистики оба этих события имеют приблизительно одинаковую вероятность. Ведь почти никто не станет задаваться вопросами, если система размещения ставок продемонстрирует чрезмерную эффективность.

Ранее я уже писал о просадках в ставках и о том, как можно управлять ими. В этой статье я хотел бы дополнить свою предыдущую работу, выполнив простое моделирование проигрышных последовательностей, а также более точно рассчитав математическое ожидание возможной длительности подобной череды неудач.

С целью упрощения понимания я постараюсь ограничить масштабность исследования. Я смоделирую k последовательных проигрышей в выборке из n обладающих одинаковыми коэффициентами ставок: впрочем, вам ничего не мешает расширить эту модель для изучения более сложных проигрышных последовательностей в более комплексных историях размещения ставок с различными коэффициентами. Для этого просто выполните моделирование по методу Монте-Карло. Впрочем, при максимально простой череде неудач можно вывести базовую математическую формулу для описания закономерности, чего не так-то просто добиться при более сложных последовательностях.

Вероятность проигрыша

Предположим, что мы рассматриваем историю размещения ставок такого игрока, уровень профессионализма которого позволяет добиться безубыточности в долгосрочной перспективе. Другими словами, этому игроку удается размещать ставки при справедливых коэффициентах. Таким образом, используемые им коэффициенты будут отображать «истинную» вероятность исхода события. На самом деле, как покажут дальнейшие расчеты, результаты исследования для непрофессиональных игроков, размещающих ставки с маржой, не сильно отличаются от результатов для компетентных игроков, которым удается достичь гарантирующего прибыль математического ожидания. Причина этому проста: большинство происходящих в сфере размещения ставок событий подвержено влиянию случайности. Коэффициенты величиной 2,0 соответствуют вероятности в 50 %, коэффициенты величиной 4,0 соответствуют 25 % и т. д. Вероятность выигрыша для k последовательных ставок с одинаковыми коэффициентами o можно рассчитать следующим образом:

Например, вероятность пяти последовательных выигрышей для ставок «один к одному» при справедливых коэффициентах величиной 2,0 составляет 1/32.

Но нас куда больше интересуют проигрыши по ставкам. При коэффициентах на победу величиной 2,0 коэффициенты на проигрыш будут также равняться 2,0, так как вероятность и победы, и проигрыша составляет 50 %. Впрочем, гораздо чаще коэффициенты на победу не соответствуют коэффициентам на проигрыш. Учитывая тот факт, что вероятность проигрыша равна единице, из которой вычли вероятность выигрыша, коэффициенты на проигрыш можно рассчитать с помощью следующего выражения:

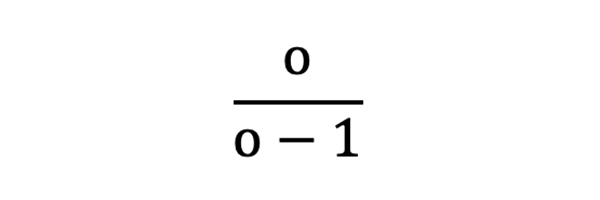
Таким образом, вероятность проигрыша для k последовательных ставок с одинаковыми коэффициентами o можно рассчитать следующим образом:

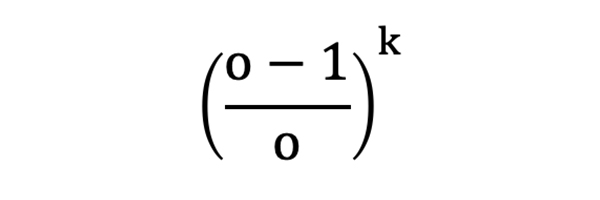
Математическое ожидание для проигрышных последовательностей

Какова вероятность наличия k (или более) последовательных проигрышей в выборке из n ставок с коэффициентами o? Как выяснилось, математические расчеты для этого случая нетривиальны и даже выходят за рамки моей работы. Но можно немного изменить формулировку этого вопроса, что существенно понизит сложность соответствующих расчетов. Давайте попробуем выяснить следующее: в скольких случаях можно ожидать k последовательных проигрышей в выборке из n ставок с коэффициентами o?

Рассмотрим простой пример. Как часто можно столкнуться с тремя последовательными проигрышами для ставок с коэффициентами 2,0 в серии из 10 ставок? Нам уже известно о том, что вероятность возникновения однократной последовательности из трех проигрышей подряд составляет 1/8. Тем не менее в серии из 10 ставок возникновение последовательности из трех проигрышей подряд может случиться множеством различных способов. Подобную череду мы можем наблюдать в ставках с первой по третью, со второй по четвертую и так далее, вплоть до ставок с восьмой по десятую.

В этом примере у нас есть восемь возможных последовательностей, так что предполагаемая вероятность возникновения подобной последовательности в 10 ставках соответствует 8/8 или же единице. Говоря другими словами, в среднем можно ожидать возникновения одной последовательности из трех проигрышей в каждых десяти ставках. Иногда их будет больше, иногда их не будет вовсе, но усредненный результат все равно будет равен единице.

В обобщенном случае количество возможных расположений такой последовательности в серии из n ставок соответствует n – (k – 1) или же n – k + 1.

Исходя из этого можно рассчитать ожидаемое количество k последовательных проигрышей (назовем его e_k) в выборке из n ставок:

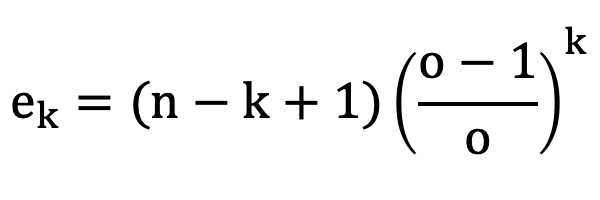
При увеличении количества ставок (n) и малых значениях k (а значение k всегда будет гораздо меньше n, так как величина интересующих нас и реалистично возможных последовательностей достаточно мала) значение e_k будет стремиться к следующим показателям:

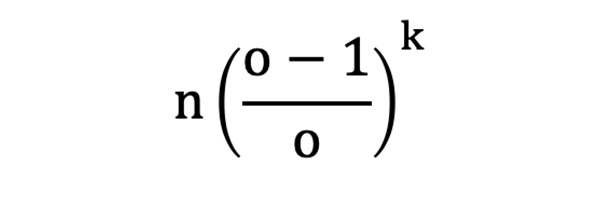
Например, для выборки из 1000 ставок с коэффициентами 2,0 количество ожидаемых проигрышных последовательностей из пяти ставок будет соответствовать 31,25 (31,125, если использовать более точную формулу), что можно округлить до 31 – ближайшего целого числа.

Так как количество ставок (n) прямо пропорционально соответствует ожидаемому количеству проигрышных последовательностей длиной в k ставок, можно предполагать наличие около 62 последовательностей из пяти проигрышей для 2000 ставок и наличия около 93 последовательностей для 3000 ставок.

При e_k = 1 величина k представляет собой длину максимальной из проигрышных последовательностей, которую можно ожидать в выборке из n ставок. Почему дела обстоят именно так? При значении менее единицы мы не столкнемся с этой последовательностью, при превышающем единицу значении есть вероятность возникновения более продолжительной последовательности проигрышей, но ее повторений при этом будет куда меньше.

При n >> k и e_k = 1:  мы получим следующие результаты:

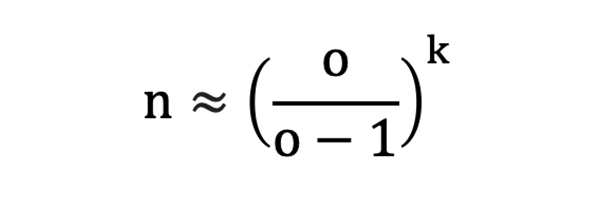
Перепишем формулу в ином виде:

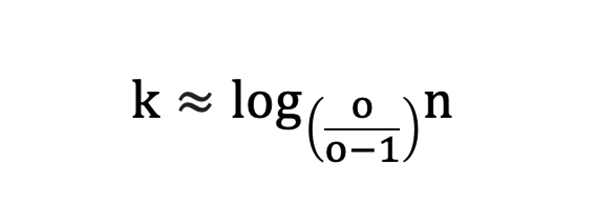
где  представляет собой основание логарифма.

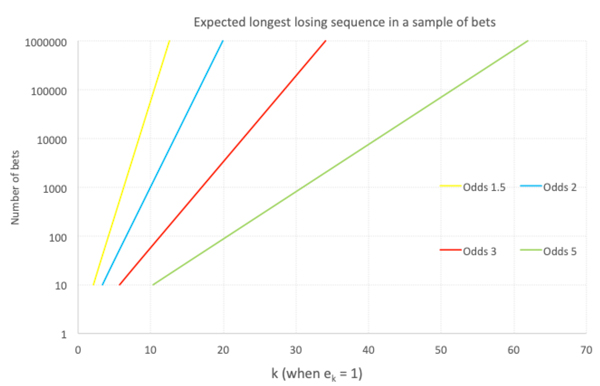
Для 1000 ставок с коэффициентами 2,0 ожидаемая длиннейшая последовательность проигрышей будет соответствовать log₂1000 = 9,97 или же 10 (вновь округляем до ближайшего целого числа). Другими словами, имея дело с выборкой из 1000 ставок, можно предполагать, что длиннейшая последовательность проигрышей будет состоять из 10 ставок.

Для коэффициентов величиной 3,0 ожидаемая длиннейшая последовательность проигрышей будет соответствовать 17, а для коэффициентов величиной 5,0 – 31. Равные 5,0 коэффициенты довольно типичны для ставок на скачки. Уверены ли вы в том, что вам удастся смириться с 31 последовательным проигрышем, и при этом вы вовсе не обольетесь холодным потом при размещении очередной ставки?

Я провел моделирование по методу Монте-Карло с 10 000 итераций и проверил свои математические расчеты для e_k. В приведенной ниже таблице сравниваются результаты для различных значений k. Можно проследить практически идеальное соответствие между показателями, полученными с помощью расчетов по используемой нами ранее математической формуле для определения проигрышных последовательностей, и итогами моделирования по методу Монте-Карло.

На приведенном ниже графике я продемонстрировал зависимость между k и e_k для различных коэффициентов на победу. Ось Y (величина e_k) является логарифмической. Прямая линия подтверждает, что величина k обратно пропорциональна логарифму e_k – именно этого можно было ожидать на основании математических расчетов. Точка, в которой каждая линия пересекает ось X (e_k = 1), соответствует ожидаемой длиннейшей последовательности проигрышей.

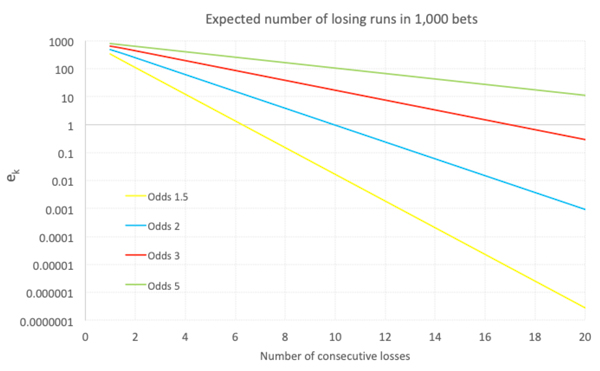
Учитывая продемонстрированное отклонение величины k, можно утверждать, что ожидаемая длиннейшая последовательность проигрышей в выборке из n ставок также пропорциональна логарифму n, что подтверждается приведенным ниже графиком. Таким образом, значение k удваивается при каждом возведении значения n в квадрат.

Вероятность возникновения проигрышной последовательности

Знание ожидаемого количества проигрышных последовательностей – это, конечно же, полезно, но нам все еще неизвестно, насколько вероятно появление подобной последовательности. Как уже упоминалось ранее, математические расчеты для определения этой величины нетривиальны, так как распределение частот (вероятностей) для количества проигрышных последовательностей длинной k в выборке из n ставок представляется неочевидным и будет сильно отличаться в зависимости от диапазонов значений k.

Например, нам может быть известно, что в среднем мы столкнемся с одной последовательностью проигрышей в рамках 10 ставок, относящихся к выборке из 1000 ставок «один к одному», но это всего лишь средний показатель. Довольно часто подобные последовательности будут отсутствовать, порой мы увидим сразу две, а иногда – пять или больше. Куда проще снова довериться нашему испытанному моделированию по методу Монте-Карло.>

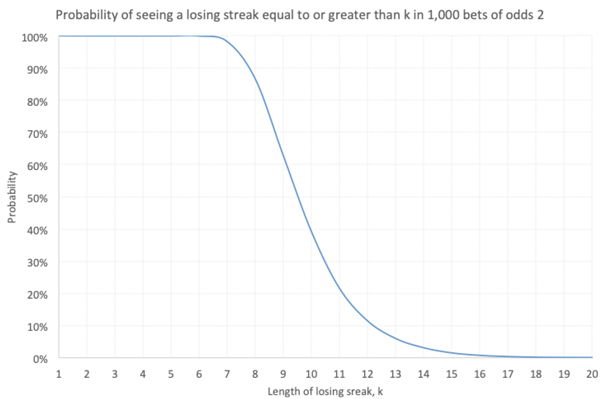
Благодаря 10 000 запусков использующей метод Монте-Карло модели я вычислил количество случаев, в которых последовательность проигрышей длиной k не наблюдалась. Например, для k = 10 и выборке из 1000 ставок «один к одному» длиннейшая проигрышная последовательность оказывалась короче ожидаемой в 6086 случаях, но равнялась как минимум 10 во всех остальных прогонах модели.

С учетом закона больших чисел можно утверждать, что возникновение проигрышной последовательности длиной не менее 10 ставок происходит с вероятностью, приблизительно равной 39 %. На интуитивном уровне это выглядит правдоподобно: мы помним, что расчеты указывают на возникновение проигрышной последовательности из 10 ставок в такой выборке примерно один раз. На приведенной ниже диаграмме отражена зависимость возникновения последовательности из k или больше проигрышей от величины k.

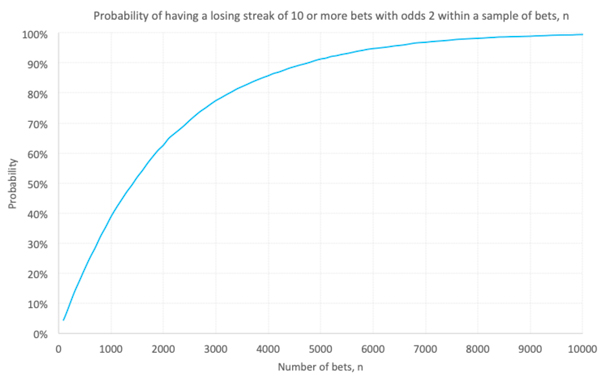
Вполне очевидно, что чем крупнее выборка, тем больше вероятность того, что в определенный момент игроку может крупно не повезти. Нам известно, что вероятность возникновения 10 последовательных проигрышей в выборке из 1000 ставок «один к одному» составляет 39 %. Чему будет равняться этот показатель при уменьшении или увеличении выборки? Для нахождения ответа на этот вопрос я провел еще одно моделирование по методу Монте-Карло. Ниже приведена диаграмма для k = 10.

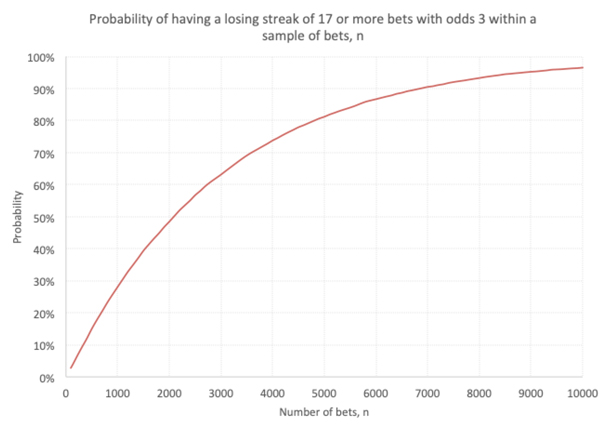
Можно выполнить аналогичное моделирование для любого другого k или другого набора коэффициентов. Ниже приведены результаты для коэффициентов 3,0 и проигрышной последовательности длиной не менее 17 ставок.

Анализ проигрышных последовательностей на реальных примерах из истории размещения ставок

До сих пор наш анализ опирался исключительно на теорию: мы рассматривали выборки ставок, в которых коэффициенты оставались неизменными. Эти данные хорошо отражают реальность для ставок на разницу в счете и ставок с азиатским гандикапом, но они плохо применимы для денежных линий и фиксированных коэффициентов: при размещении ставок последних двух типов игроки сталкиваются с огромным разнообразием коэффициентов. Например, в моей системе размещения ставок Wisdom of the Crowd есть матчи с коэффициентами от 1,11 до 67,0 с усредненным значением 3,9 и стандартным отклонением, превышающим 4,0.

Конечно же, можно было бы использовать моделирование по методу Монте-Карло для определения ожидаемой проигрышной последовательности, но сохраняется ли у нас возможность прибегнуть к математическим расчетам? Ответ – да, нам всего лишь нужно внимательно выбирать подходящее значение для выражающей коэффициенты величины o. Мы не можем использовать усредненные коэффициенты для нашей выборки, так как результат будет непропорционально перекошен в сторону более высоких коэффициентов.

Вместо этого необходимо прибегнуть к использованию инверсии усредненных предполагаемых вероятностей для всех коэффициентов. К примеру, если в нашей выборке есть пять ставок с коэффициентами 2,0, 3,0, 5,0, 10,0 и 20,0, следует рассчитать предполагаемые вероятности (0,5, 0,333, 0,2, 0,1 и 0,05), вычислить их среднее арифметическое (0,237) и выполнить его инверсию (o = 4,23).

Я выполнил все эти операции для моей системы Wisdom of Crowd, которая содержит выборку из 9436 ставок. Использование рассчитанного с помощью указанного выше метода значения o = 2,66 демонстрирует идеальное соответствие ожидаемых значений k и реальных проигрышных последовательностей.

Математические расчеты указали на наличие 898 проигрышных последовательностей из пяти или более ставок, а в реальности их было 889. Подобным образом, для k = 10 математические расчеты указали на значение 85; и в реальности действительно существовало 85 соответствующих последовательностей. Для k = 9 спрогнозированное значение равнялось восьми, в реальности оно было равным девяти. Ожидаемая длиннейшая проигрышная последовательность (e_k = 1) по прогнозам соответствовала 19. Она действительно состояла из 19 ставок и возникла лишь однажды.

Что же насчет последовательностей выигрышей?

Можно использовать аналогичные расчеты для изучения математического ожидания последовательностей выигрышей. И это даже потребует меньших усилий: можно подставить коэффициенты на победу напрямую в формулу, не тратя время на преобразование их в коэффициенты на проигрыш. Нужная формула будет выглядеть так:

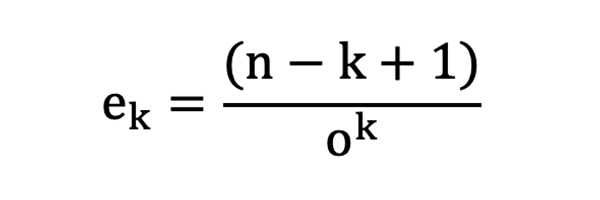
И для e_k = 1:

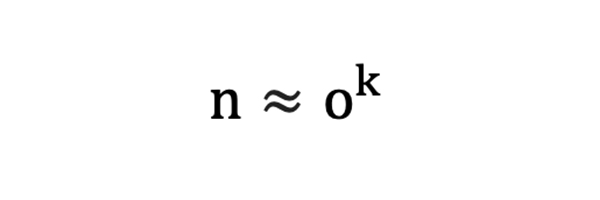
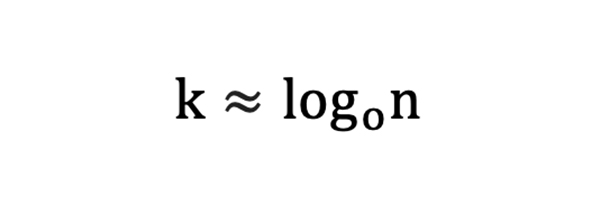
Тем не менее для анализа выборок с разнородными коэффициентами необходимо помнить о важности использования подходящего значения o, которое должно представлять собой не усредненные коэффициенты, а инвертированное значение усредненных предполагаемых вероятностей.

Так что же мы узнали о проигрышных последовательностях в размещении ставок?

При размещении ставок на протяжении длительного времени неизбежно приходится сталкиваться с неудачами. Я надеюсь, что этот относительно теоретический анализ последовательностей в размещении ставок послужит для вас напоминанием о том, что чем дольше вы размещаете ставки, тем более вероятной становится ваша встреча с достаточно длинными последовательностями проигрышей.

Каждый успешный игрок должен не только отыскивать предположительно ценные ставки, но и в разумной мере сдерживать свои ожидания, а также уметь справляться с неизбежными последовательностями неудач, которые могут существенно повлиять на психологическое состояние игрока. Знание о том, чего ожидать от ставок и как оценивать результаты, сможет по меньшей мере подготовить вас к будущим неудачам.

JOSEPH BUCHDAHL