Pinnacle … Еще одна точка зрения на случайность и эффективность в ставках на футбол

Мне кажется, многим читателям уже надоели поучения о том, как сложно размещать ставки на футбольные матчи из-за случайности и эффективности рынков. Я тоже так думал, но в условиях карантина и отсутствия футбольных матчей, когда мне нечем заняться, кроме как откладывать написание очередной книги, я вспомнил некоторые старые идеи.

Перед вами результат этой работы. В этой статье практически нет новых идей — лишь другая точка зрения на них. Надеюсь, она будет вам полезна.

Как выглядит эффективность?

Уже много лет мне приходится спорить с людьми, которые утверждают, что в футболе нет места случайности. Откуда ей взяться, если «Манчестер Юнайтед» имеет такой высокий шанс победить «Кембридж Юнайтед»? Они правы. Но мы говорим не о футболе, а о ставках на футбол.

В них коэффициенты корректируются с учетом разницы в способностях команд. Чем лучше команда, тем ниже коэффициент. Когда достаточно людей выразят свои мнения о шансах команд на победу с помощью денег, коэффициенты становятся довольно близки к «настоящим» (если бы их можно было узнать) в ходе процесса, который называется определением цен. Не важно, чьими мнениями руководствуется букмекер: широкой публики или профессиональных игроков.

Цель букмекера — максимально приблизиться к настоящим коэффициентам, сведя к минимуму риск и заработав свою комиссию маркетмейкера в долгосрочной перспективе. Цель игрока — обнаружить его ошибки.

Один из способов определить, приближается ли букмекер (в среднем) к настоящим коэффициентам, — проверить, покроются ли расходы, если выставить эти коэффициенты на рынок еще до применения маржи. Кроме того, если варьирование прибыли для небольших наборов ставок распределяется так же, как и при бросках симметричных монет, и эти доходы снижаются до средних, это еще один признак того, что коэффициенты эффективны, а варьирование результатов — это просто шум, а не сигнал.

Давайте взглянем на данные. Изучив последние три завершенных сезона (с 2016–2017 до 2018–2019 годов) профессиональных футбольных лиг Англии, я использовал коэффициенты Pinnacle при закрытии без маржи («честные» коэффициенты), чтобы рассчитать показатели команд в каждом матче. Простое правило расчета этого показателя, которое я уже использовал раньше, выглядит так.

Если команда выиграла, начисляется 1 – 1/коэффициент.

Если команде не удается выиграть, начисляется –1/коэффициент.

Таким образом, показатель команды в отдельных матчах теоретически может находиться в пределах от +1 до –1.

Для четырех дивизионов за три сезона (6108 матчей и 12 216 показателей) среднее значение составляет 0,0030 при стандартном отклонении 0,4557. Это довольно близко к показателю 0, который получится, если честные коэффициенты будут идеальными (в среднем).

Случайное распределение показателей?

А что насчет распределения выборок показателей? Упорядочив данные по команде и дате матча, я рассчитал серию скользящих средних показателей за шесть матчей для каждой команды. Естественно, в течение первых пяти матчей сезона рассчитать этот показатель невозможно.

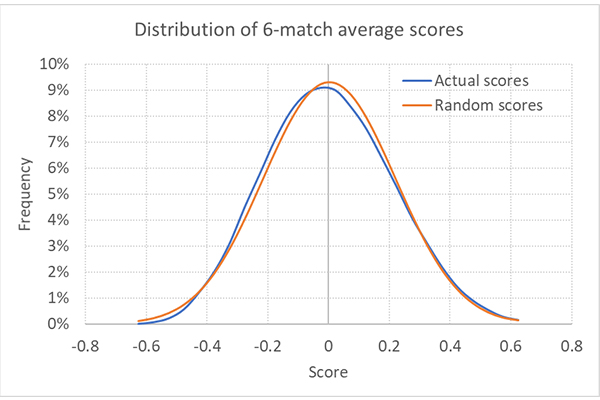
Средний показатель за шесть игр составляет 0,0032 при стандартном отклонении 0,1866. На приведенной ниже схеме их распределение обозначено синей линией. Оранжевая линия обозначает теоретическое нормальное распределение случайно сгенерированных показателей. Нам нужно определить отличия между ним и распределением показателей, основанных на фактических результатах.

Кроме того, стандартное отклонение почти идентично прогнозируемому согласно первым принципам с использованием стандартной погрешности среднего значения:

где σ — это стандартное отклонение показателей для всей совокупности отдельных матчей, а n — это размер выборки (в данном случае 6). Таким образом:

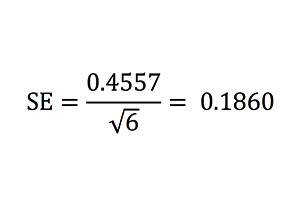
Это сильно отличается от наблюдаемого показателя 0,1866. Мы можем снова воспользоваться формулой стандартной погрешности, чтобы рассчитать ожидаемое стандартное отклонение этого показателя стандартной погрешности, то есть стандартную погрешность стандартной погрешности. Учитывая, что у нас есть 10 836 выборок по 6 игр, расчеты будут выглядеть так:

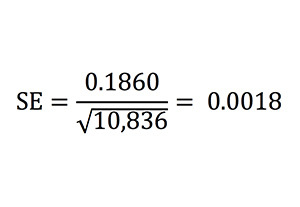
Следовательно, значение 0,1860 отличается от 0,1866 лишь на треть стандартного отклонения, то есть вполне в рамках статистической значимости. Разница между наблюдаемой и ожидаемой случайностями возникла по стечению обстоятельств.

Из этого можно сделать вывод, что коэффициенты Pinnacle отлично отражают реальную ситуацию, а результаты, которые большинство игроков получат от этих ставок (по крайней мере в течение шести матчей), зависят от везения.

Это очень неутешительный вывод, за который меня постоянно критикуют. В основном претензии относятся к фразе «в среднем». Коэффициенты Pinnacle для футбольных матчей могут быть эффективными в среднем, но игроки ставят не на средние показатели. Конечно, это так, но проблема игрока состоит в том, как систематически обнаруживать конкретные ошибки букмекера. Опыт показывает, что большинство игроков «находят» их произвольно.

Я повторил этот эксперимент для серий из 12 и 24 игр. Распределение показателей показано ниже. Оно соответствует нормальным распределениям случайно сгенерированных значений еще больше, чем показатели для шести игр.

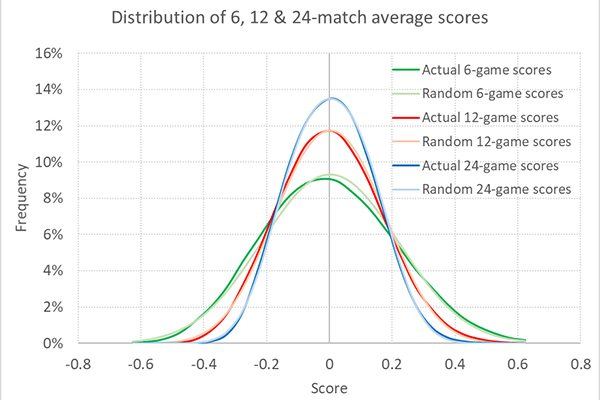
Средние показатели для 12 и 24 игр составляют 0,0037 и 0,0049 соответственно (небольшие отличия между тремя значениями, скорее всего, связаны со случайностью и разным размером выборок матчей). Стандартные отклонения составляют 0,1301 и 0,0916, соответственно, а при расчете с использованием стандартной погрешности среднего значения, — 0,1315 и 0,0930. Они отличаются от ожидаемых значений примерно на 1 стандартное отклонение, то есть разница снова вызвана исключительно случайностью.

Регрессия к среднему значению

Если бы отклонения в показателях за шесть игр были систематическими, то мы могли бы предсказать исход. Например, от команд, которые пребывали в хорошей форме на протяжении шести игр, показывая положительную среднюю оценку, можно было бы ожидать положительного среднего результата и за следующие шесть игр. К сожалению, это не так. В выборках из шести игр наблюдается почти идеальная регрессия к среднему значению.

Однако я не пытаюсь сказать, что команды, которые были лучше других в шести играх, начнут сдавать позиции в течение следующих шести матчей. Наоборот, сильные команды обычно остаются сильными. Достаточно взглянуть на результаты клуба «Ливерпуль» в этом сезоне. Я утверждаю, что заработанные при этом очки, которые компенсируются на рынке ставок с учетом способностей команды, регрессируют к среднему значению.

Приведенная ниже схема показывает, что в общем случае практически невозможно предсказать, каким будет средний результат команды с 7-го по 12-й матч, руководствуясь показателями за первые шесть игр. Серии побед могут быть у футбольных команд, но не у игроков, делающих ставки с форой.

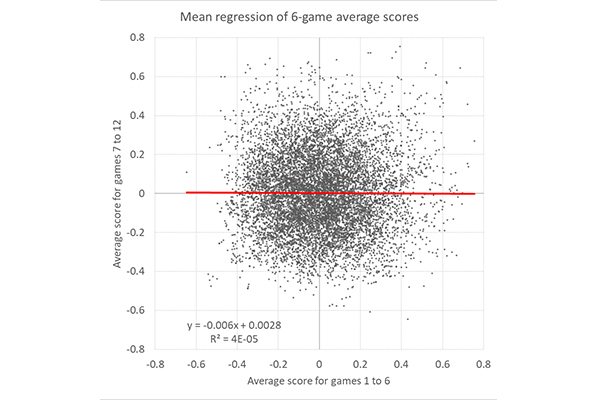
Умение букмекеров устанавливать коэффициенты и способность игроков пользоваться выявленными ошибками приводят к тому, что к моменту закрытия рынка почти все оставшиеся отклонения коэффициентов являются результатом естественной неопределенности, или просто случайности.

Правило оценки?

В прошлом месяце я рассматривал использование показателя вероятности ранга (RPS) в качестве правила оценки, которое помогает измерять эффективность рынка Pinnacle для ставок на футбол. Правило оценки, которое мы использовали в этой статье, можно рассматривать аналогичным образом.

Если бы коэффициенты Pinnacle были абсолютно эффективными, то средний показатель для выборки составлял бы ровно 0. Конечно, что касается RPS, мы никогда не узнаем, в какой степени отклонение от значения 0 является результатом естественной неопределенности (случайности результатов), а в какой — результатом эпистемической неопределенности (ошибки в используемой букмекером модели определения коэффициентов). При удалении маржи из коэффициентов Pinnacle я мог внести дополнительную эпистемическую погрешность. Так как нам неизвестно, как именно букмекеры применяют маржу, пришлось воспользоваться предположительным алгоритмом.

Как бы то ни было, приближение среднего показателя выборки к 0 и близость распределений примеров средних показателей за матч к случайному распределению являются убедительным аргументом в пользу эффективности коэффициентов Pinnacle для ставок на футбольные матчи.

А что насчет ошибки «череды удач»?

В результате этого эксперимента остается нерешенная проблема. Два года назад я представил систему ставок, которая пыталась воспользоваться неэффективностью коэффициентов Pinnacle на футбольные матчи, возникающей из-за ошибки «череды удач».

Гипотеза заключалась в том, что игроки могут верить в полосы везения. Следовательно, они могут слишком много ставить на команды с сериями побед, снижая коэффициенты относительно фактических вероятностей соответствующих исходов. С другой стороны, ставок на менее удачливые команды может быть слишком мало, что повышает их коэффициенты и создает выгодные возможности.

Разница между ставками на относительно невезучие команды и ставками на клубы, одерживающие много побед подряд, в сериях из 6 матчей была весьма незначительной (p = 0,02 для проанализированной выборки матчей). При сравнении самых худших команд с самыми лучшими отличие было намного больше (p = 0,001), а коэффициенты Pinnacle при закрытии могли бы принести фактическую прибыль в размере 2,7 % для выборки из более чем 5000 ставок (при среднем коэффициенте 3,9). Но что, если этот анализ представляет рынок как почти идеально эффективный? Все это было лишь приятной иллюзией?

Это возможно. Эта прибыль в размере 2,7 % может произвольно возникать в 7 из 100 случаев, поэтому с точки зрения статистики ее нельзя назвать гарантированной. Однако если опять внимательно изучить средние показатели за 6 игр, можно увидеть, что крупных отрицательных результатов намного меньше, чем ожидается при случайном распределении. 438 из них были меньше, чем –0,3, но при случайном распределении таких показателей было бы 563.

Это можно объяснить тем, что игроки мало ставят на команды, проигрывающие много раз подряд, поэтому коэффициенты этих клубов растут больше, чем следовало бы. Таким образом, с каждым поражением они получают относительно небольшую отрицательную оценку. Поставив на эти 438 команд, чей средний показатель за 6 игр составляет менее –0,30, в их 7-м матче, мы получили бы прибыль в размере 11,6 % (при среднем коэффициенте 3,22 и p = 0,06).

Вообще-то, лишь 438 показателей менее –0,3 — весьма удачный результат. С такими коэффициентами случайный выбор результатов согласно их предполагаемым вероятностям показал ожидаемое значение 513, и лишь в 2,5 % испытаний методом Монте-Карло показателей было меньше, чем 438. Теперь мы можем сравнить это число (513) с ожидаемым значением при идеальном нормальном распределении и среднем показателе выборки, равным 0. Это значение составляет 584. Лишь в 3,5 % испытаний модели получилось больше 584 средних показателей за шесть игр, составляющих менее –0,3. Специалисты по статистике назвали бы этот процент малозначимым. Возможно, распределение фактических показателей за 6 игр все-таки не случайно.

Конечно, такая же логика должна быть применима к «везучим» командам. При последовательных победах коэффициенты должны снижаться относительно фактических вероятностей соответствующих исходов, то есть высоких положительных показателей тоже должно становиться меньше. Но в этом образце данных наблюдается другая тенденция.

Еще подробнее о случайности и эффективности в ставках на футбол

Если в распределении показателей для ставок на футбол и есть что-то неслучайное, то наш анализ показывает, что найти этот фактор сложно. Действительно, существует тонкая грань между случайным шумом и потенциально выгодным систематическим сигналом, который станет заметен только самым талантливым и трудолюбивым игрокам после продолжительных экспериментов.

Перед вами результат этой работы. В этой статье практически нет новых идей — лишь другая точка зрения на них. Надеюсь, она будет вам полезна.

Подведем итоги: очевидно, что коэффициенты Pinnacle очень эффективны (хотя бы в среднем), а систематические огрехи (одним из которых является ошибка «череды удач») трудноуловимы. Кроме того, по большей части Pinnacle хорошо следит за тем, чтобы даже при наличии таких ошибок они оставались в допустимых пределах. Определить коэффициенты точнее, чем Pinnacle (по крайней мере, для английских футбольных лиг), — задача не из простых.