Pinnacle … Сколько нужно ставить, если вы не знаете свои шансы на успех?

В мае 2020 года два акционера типстерской платформы Pyckio (Андрес Барж-Жиль и Альфредо Гарсия-Иерно) опубликовали в журнале Journal of Sports Economics исследование того, как успешный игрок должен рассчитывать ставки, если прогнозы вероятности выигрыша недоступны.

Вопрос о том, стоит ли вообще игроку, стремящемуся к стабильной прибыли в долгосрочной перспективе, действовать в таких условиях, является спорным, но, как утверждают Барж-Жиль и Гарсия-Иерно, многие игроки признают, что не могут точно их оценить.

Тем не менее их исследования интересны тем, что показывают, как можно по-новому интерпретировать различные стратегии ставок в виде вариаций критерия Келли. В этой статье я хочу вкратце рассказать об их работе и попробовать усовершенствовать их метод.

Новая интерпретация различных стратегий ставок с использованием критерия Келли

Что касается управления финансами при размещении ставок на спорт, наверное, нет более популярной темы, чем использование критерия Келли для расчета ставок. Действительно, в разделе «Ресурсы для размещения ставок» на сайте Pinnacle есть множество статей на эту тему. Даже я написал парочку. В частности, я продемонстрировал, что для простого расчета ставок по критерию Келли, когда ставки размещаются по одной, стратегия позволяет компенсировать риск, связанный с тем, что вам неизвестны точные преимущества, при условии что в среднем ваши расчеты точны.

В своей статье Барж-Жиль и Гарсия-Иерно утверждают, что когда точные вероятности неизвестны, игроки отказываются от критерия Келли и прибегают к другим планам управления финансами.

Удельные убытки

Первый из них — метод удельных убытков, или равных ставок. При этом игрок ставит одну и ту же сумму во всех случаях, независимо от коэффициентов. Чем выше коэффициент, тем больше прибыль в случае выигрыша, но меньше его вероятность.

Мы можем рассматривать ставки по методу удельных убытков как план с использованием критерия Келли, где ожидаемый доход прямо пропорционален коэффициенту. Так как размер ставки по критерию Келли рассчитывается по формуле «ОД / коэффициент – 1» (где ОД — ожидаемый доход, любое положительное значение которого считается прибыльным), метод удельных убытков предполагает, что это соотношение остается неизменным.

Допустим, ОД составляет 10 % (0,1), а коэффициент — 2,00. Размер ставки будет равен 0,1. Если повысить коэффициент до 4,00, то ОД должен увеличиться до 30 % (0,3), чтобы размер ставки остался равным 0,1. Коэффициент 101,00 подразумевает, что ОД равен 10, или 1000 %, что немного нереалистично. Это означает, что фактический коэффициент составляет лишь 9,18. Конечно, ни один букмекер не совершит такую ошибку.

Действительно, если коэффициент стремится к бесконечности, то фактический коэффициент будет стремиться к максимальному значению выражения «1 / ставка», в данном случае 10. Серьезный недостаток метода удельных убытков заключается в том, что при ставках на маловероятные исходы риск слишком высок. Для сторонников критерия Келли это было бы логично, только если бы ОД действительно увеличивался пропорционально коэффициенту. Как видите, это совсем не так.

Удельная прибыль

Вторая распространенная стратегия управления финансами — метод удельной прибыли. В этом случае игрок стремится получить одинаковую прибыль вне зависимости от коэффициента. Если целевой выигрыш, или прибыль, составляет 100 евро, то при коэффициенте 2,00 необходимо поставить 100 евро, а при коэффициенте 5,00 — 25 евро. Размер ставок пропорционален обратной величине коэффициента – 1. С точки зрения критерия Келли, метод удельной прибыли предполагает, что между ОД и критерием Келли нет корреляции. ОД остается одинаковым независимо от коэффициента.

Что касается расчета ставок по методу удельной прибыли, что-то тут не так. Действительно ли преимущество игрока будет одинаковым при коэффициентах 1,11 и 111,00? Дисперсия показывает, что это предположение нереалистично. В самом деле, если бы ОД при коэффициенте 111,00 составлял 20 % (0,2), то такой же ОД при коэффициенте 1,11 означал бы, что фактический коэффициент меньше 1, что совершенно бессмысленно. Вероятность какого-либо исхода не может быть больше 100 %.

Удельное влияние

Барж-Жиль и Гарсия-Иерно предложили альтернативный план расчета ставок — метод удельного влияния, предполагая, что этот план лучше сочетается с методом расчета на основе критерия Келли. В методе удельного влияния разница в банкролле между выигрышем и проигрышем остается неизменной вне зависимости от коэффициента.

При этом размер ставки обратно пропорционален коэффициенту, в отличие от метода удельной прибыли, где он пропорционален обратной величине коэффициента – 1. Таким образом, если сумма ставки составляет 100 евро при коэффициенте 2,00, то при коэффициенте 5,00 она будет составлять 40 евро. В каждом случае разница между выигрышем и проигрышем составляет 200 евро (+100/–100 евро в первом случае и +160/–40 евро во втором).

В методе удельного влияния ОД пропорционален выражению «коэффициент – 1 / коэффициент». Это означает, что ОД увеличивается при повышении коэффициента, но его рост замедляется ближе к пределу, так как это соотношение быстро стремится к 1. Например, если ОД = 0,1 при коэффициенте 2,00, то предел ОД составляет 0,2. Хотя это не такой радикальный сценарий, как в методе удельной прибыли, где ОД остается неизменным, в нем все равно недооценивается возможность более высокого ОД при больших коэффициентах.

Прибыль успешных типстеров, специализирующихся на скачках, более чем вдвое превышает доход игроков на рынках азиатского гандикапа или ставок на разницу в счете. Однако это еще не означает, что эти игроки более искусны (или более удачливы). Просто дисперсия на их стороне.

На приведенном ниже графике показано, как ОД меняется относительно коэффициента в трех методах расчета ставок, при условии что ОД = 3 % при коэффициенте 2,00 в каждом случае.

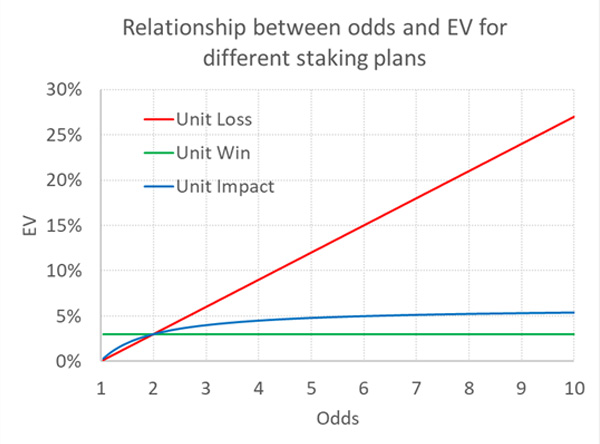Как уже упоминалось, методы удельных убытков и удельной прибыли подразумевают нереалистичное соотношение между коэффициентом и ОД.

Барж-Жиль и Гарсия-Иерно проанализировали базу данных ставок Pyckio и пришли к выводу, что соотношение между ОД и коэффициентом в методе удельного влияния наиболее точно соответствует наблюдаемым и прогнозируемым (на основе цен при закрытии) доходам типстеров. Не очень-то убедительно. Повторюсь: расчет ставок по методу удельного влияния приносит ОД, который максимум вдвое превышает ОД при коэффициенте 2,00. Есть ли альтернатива получше?

Возвращаясь к t-распределению

Три года назад я опубликовал в разделе «Ресурсы для размещения ставок» на сайте Pinnacle статью о том, как использовать t-распределение, чтобы оценивать типстеров и отличать удачу от мастерства. Подобно нормальному распределению (вместо которого оно используется, когда известно стандартное отклонение только для выборки, а не для всей совокупности), оно помогает определить вероятность той или иной выборки, при условии что известно среднее значение совокупности.

Я часто использую t-распределение в своей работе, чтобы помочь игрокам определить вероятность того, что они получили бы свои результаты при отсутствии навыков. Чем ниже эта вероятность, тем больше вы можете быть субъективно уверены, что своей прибыли от ставок вы обязаны не только удаче.

В основе этого метода лежит t-статистика или t-показатель, из которого можно получать вероятности. Я продемонстрировал, что при расчете по методу удельных убытков, если коэффициенты ваших ставок не сильно варьируются, этот показатель можно приблизительно рассчитать по следующей формуле:

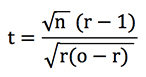
где n — это количество ставок, o — средний коэффициент, а r — возврат инвестиций или прибыль + 1.

Как и z-показатель, знакомый многим гандикаперам, он представляет собой меру количества стандартных отклонений прибыли от ожидаемого среднего значения (0), если ставки размещает неопытный игрок при честных коэффициентах. Например, если t-показатель равен 2, то при отсутствии опыта ваша прибыль могла бы быть больше только в 2,5 % случаев. Таким образом, t-показатель представляет собой меру вероятности. Чем выше t-показатель, тем менее вероятен рассматриваемый случай. Давайте определим с его помощью, насколько вероятны те или иные значения ОД (для неопытного игрока) в зависимости от коэффициентов для ставок.

Асимметрия прибыли

Допустим, вы размещаете ставку на команду, вероятность победы которой составляет 80 %, с честным коэффициентом 1,25. А теперь предположим, что букмекер ошибочно полагает, будто вероятность победы составляет 75 %. Он проводит акцию, предлагая ставки без маржи. Его коэффициент составляет 1,333. Соответственно, ОД составляет 6,667 % (1,333/1,25 – 1 или 0,80/0,75 – 1).

А теперь рассмотрим другой сценарий: фактическая вероятность равна 20 % (честный коэффициент 5,00), но букмекер считает, что она равна 15 % (опубликован коэффициент 6,667). В этом случае ОД составляет 33,33 % (6,667/5,00 – 1 или 0,20/0,15 – 1). Разница между ожидаемым вами процентом выигрыша и прогнозом букмекера остается неизменной, но ОД увеличивается в 5 раз. Похоже, с точки зрения ОД, эквивалентные ошибки имеют более серьезные последствия при более высоких коэффициентах. Но насколько вероятны такие ошибки?

Симметрия вероятности

Давайте перепишем приведенную выше формулу t-показателя (предположив, что для всех наших ставок действует один коэффициент, o). Так как нам известно, что r = q / p, где p — это вероятность, подразумеваемая коэффициентом букмекера (т. е. 1/o), а q — прогнозируемая вероятность (которая будет «правильной», если ваша модель прогнозирования точна), можно показать, что:

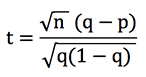
Допустим, что n, количество ставок, составляет 100. При q = 0,8 и p = 0,75 получается, что t = 1,25. Однако, аналогичным образом, при q = 0,2 и p = 0,15 также получится, что t = 1,25. При условии что букмекер, а не наша модель, оказался прав, такой t-показатель указывает, что вероятность исхода составляет 10,7 % (это значение получено с помощью функции =СТЬЮДРАСП в Excel).

Разместив более 100 ставок, мы прогнозируем прибыль более 6,667 % при коэффициенте 1,333, или более 33,33 % при коэффициенте 6,667, в 10,7 % случаев. Более высокая прибыль при больших коэффициентах так же вероятна, как и меньшая прибыль при меньших коэффициентах. Именно поэтому типстеры, специализирующиеся на скачках, выглядят лучше, чем гандикаперы, или намного хуже, когда проигрывают.

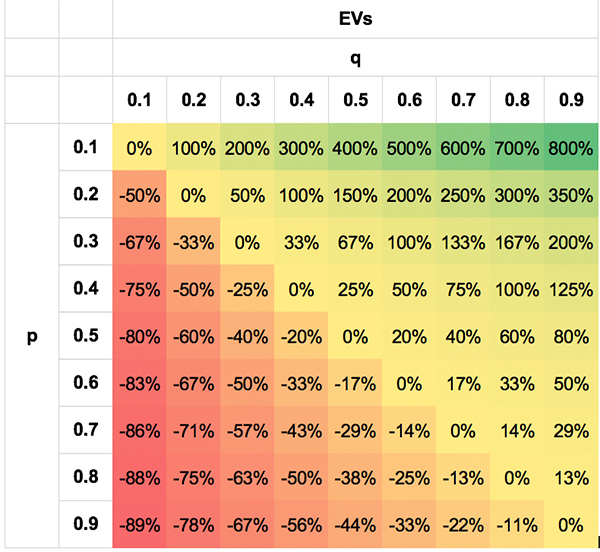
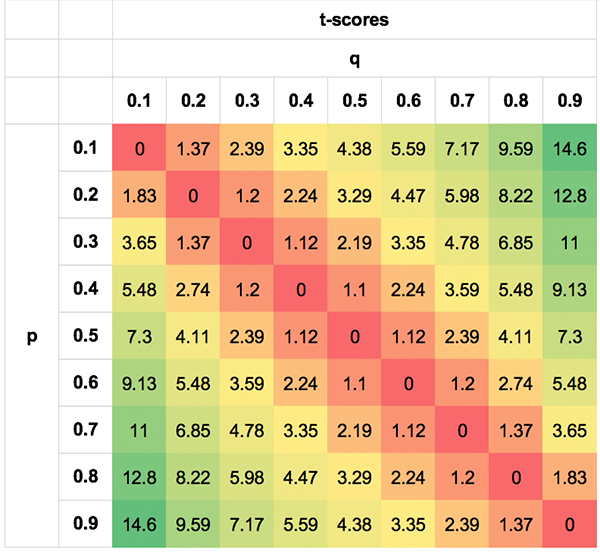
Я попытаюсь продемонстрировать эту симметрию вероятности с помощью приведенных ниже таблиц. Для наглядности выбраны экстремальные значения. Конечно, ни один игрок не сможет получить такие хорошие (или плохие) результаты в большинстве сценариев.

На первой таблице показана асимметрия ОД для разных пар p и q. На второй показана симметрия t-показателей. Для наглядности показаны абсолютные t-показатели (без знака «минус» в отрицательных значениях ОД, когда q < p). Одинаково вероятны не только пары p/q, равные 0,3/0,7 и 0,7/0,3, но и 0,7/0,5 и 0,3/0,1, 0,8/0,7 и 0,2/0,1. Причины этого уже я уже объяснил.

Новая функция ОД-коэффициента

Для заданных значений коэффициента и ОД существует вероятность t (которая удваивается при 4-кратном увеличении количества ставок). Мы можем по-другому сформулировать формулу t-показателя, выразив его через r. Получается ужасное выражение второго порядка с еще более ужасным решением.

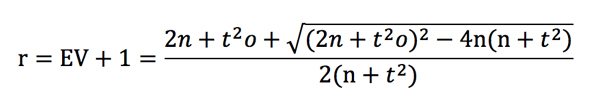
Эта формула намного сложнее, чем «коэффициент – 1 / коэффициент», но давайте все равно попробуем построить по ней график, где ОД = 0,03, а коэффициент составляет 2,00. Этот график показан ниже наряду с графиками предыдущих функций ОД-коэффициента для методов удельных убытков, удельной прибыли и удельного влияния.

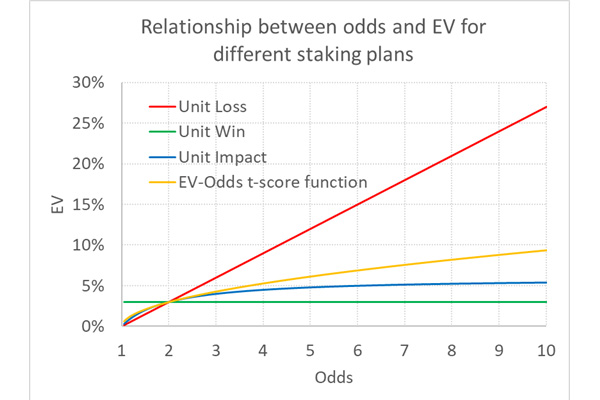
Хотя эту функцию сложно записать, она более логична, учитывая то, что прогнозируемая прибыль интерпретируется с точки зрения статистической вероятности. При расчете ставок по методу удельного влияния ОД никогда не может превышать 6 %, если он составляет 3 % при коэффициенте 2,00. Но с моей функцией он может расти бесконечно, хотя и не так нереалистично быстро, как в методе удельных убытков, но в рамках, прогнозируемых статической дисперсией. При коэффициенте 10 он составляет 9,4 %, при коэффициенте 50 — 23,3 %, а при коэффициенте 1000 — 150 %.

Очевидный недостаток этой функции, основанной на t-показателе, заключается в том, что она предполагает неопытность игрока. Она просто выражает вероятность тех или иных исходов при отсутствии навыков. Но это неправильное толкование. Даже для профессиональных игроков действуют те же статистические законы, связанные с дисперсией.

Положение оранжевой кривой изменится, но ее форма останется прежней. Ниже показаны некоторые возможные траектории в зависимости от удачи или квалификации игроков, как бы вы это ни называли. Исходная кривая для игрока с ОД, равным 3 % при коэффициенте 2,00, по-прежнему обозначается оранжевым цветом.

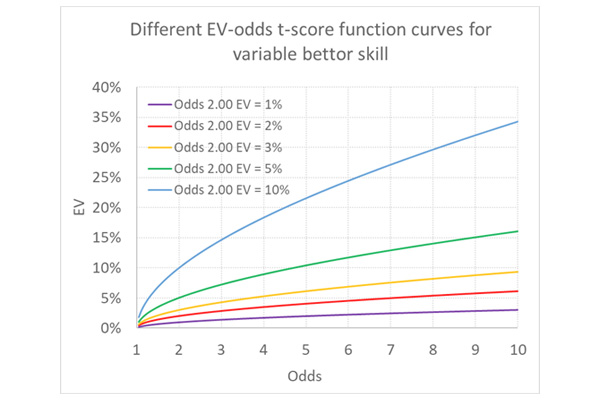
Еще один недостаток состоит в том, что предполагается, будто уровень навыков не зависит от коэффициента, то есть остается неизменным, каким бы ни был последний. Учитывая такие факторы неэффективности рынка, как предвзятость при оценке аутсайдеров и фаворитов, такое предположение может быть необоснованным.

Испытание функции

Можно ли проверить применимость этой новой функции ОД-коэффициента? Моя система коллективного мнения, знакомая тем, кто регулярно читает мои сообщения в Twitter и на сайте Football-Data, использует самые эффективные коэффициенты Pinnacle для прогнозирования ОД с коэффициентами других букмекеров.

Проанализировав подборку данных о коэффициентах на футбольные матчи европейских лиг за сезон 2012–2013 годов, я обнаружил 55 237 случаев, в которых наблюдалось прибыльное значение ОД (>0). Среднее значение составляло 2,20 % (кстати, фактическая эффективность метода удельных убытков составляла 1,77 % — вполне в рамках статической погрешности модели) при среднем коэффициенте 3,30. Используя эти значения, мы можем построить график функции ОД-коэффициента по моей формуле для корней квадратного уравнения. Он обозначен оранжевым цветом ниже.

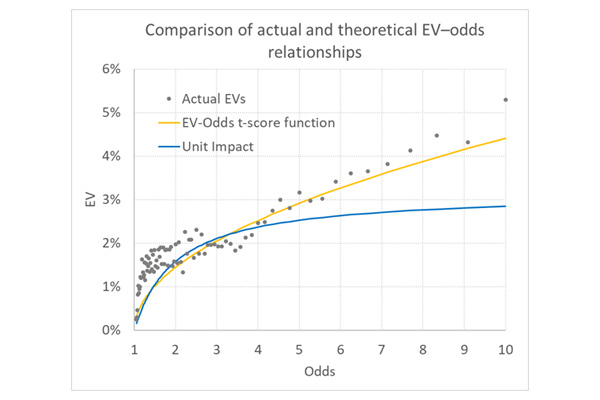
Сначала сравните его с фактическими значениями ОД в модели, когда ожидаемый шанс выигрыша равен 1 % (они представлены на схеме как коэффициенты), а затем с графиком функции ОД-коэффициента, полученным по методу удельного влияния. Конечно, совпадение не идеальное, но функция ОД-коэффициента на основе t-показателя явно намного точнее прогнозирует ОД по коэффициентам.

Обоснование

Самые наблюдательные читатели могут спросить: какой смысл использовать функцию ОД-коэффициента для прогнозирования ОД при разных коэффициентах, если метод коллективного мнения позволяет сделать это для каждой ставки? Это действительно веский аргумент, так что эту статью, по большей части, можно считать теоретической.

Тем не менее даже точные модели (в среднем) демонстрируют гносеологическую неопределенность от ставки к ставке. Более того, случайная (или неизбежная) неопределенность делает расчет фактической вероятности выигрыша невозможным.

Цель этого эксперимента (как и исследования, которое провели Барж-Жиль и Гарсия-Иерно) — продемонстрировать, как можно приблизительно рассчитать ОД, принимая во внимание количественную неопределенность, если ваша модель прогнозирования не позволяет прогнозировать вероятность выигрыша в явном виде или ваш метод скорее является качественным, то есть больше основан на интуиции, чем на анализе данных. Если вам известны коэффициенты, с помощью этого метода вы можете примерно рассчитать ОД. Зная ОД, вы можете вычислить размер ставки по критерию Келли.

Метод с использованием t-показателя может показаться запутанным, но его результаты основаны на более логичных выводах о соотношении между вероятностью выигрыша, ожидаемым доходом и вероятностью исхода, а значит, и варьировании фактической прибыли в зависимости от коэффициентов. Мне кажется, этот способ лучше подойдет сторонникам критерия Келли, чем метод удельного влияния, и уж точно лучше, чем методы удельных убытков и удельной прибыли.

JOSEPH BUCHDAHL