Pinnacle … Асимметрия букмекерства

В месяцы спортивного затишья я задумывался о том, можно ли измерить уровень игроков, необходимый для победы над букмекерами. Как обычно, я говорю не о везении, а о долгосрочной ожидаемой прибыли на основе стратегии ставок на завышенные коэффициенты.

Как известно, для этого нужно перекрыть букмекерскую маржу. То, что добиться подобного результата удается лишь незначительной части игроков, свидетельствует о том, что это задача не из легких даже в тех случаях, когда маржа невелика и составляет всего 2 %.

В своих статьях и публикациях в Twitter я упоминал о нескольких инструментах Excel. С их помощью я измеряю статистическую вероятность достижения положительного значения EV, а также прогнозирую распределение результатов с учетом определенных предположений касательно ставок.

Но в этот раз я хочу исследовать именно превосходство над букмекером в контексте неопределенности. Как мы знаем, ставки связаны с неопределенностью. С ней неизбежно сталкиваются даже самые лучшие игроки. До какой степени нужно снизить неопределенность, чтобы перекрыть маржу и побеждать в течение длительного периода?

Если пытаться смоделировать ответ, то станет ясно, насколько сильны в действительности букмекеры и почему им нужно таковыми быть, чтобы оставаться в плюсе. Это асимметрия букмекерства.

Два вида неопределенности

В своих двух последних статьях для Pinnacle я рассмотрел два вида неопределенности. Первая называется случайной, или статистической. Это естественная неопределенность, обусловленная изменчивостью вероятности. Если многократно повторить процесс, например подбросить монету, то незначительные различия в начальных условиях приведут к разным результатам. Такие различия остаются неизвестными. Уменьшить случайную неопределенность невозможно.

Некоторые, например вымышленный демон Лапласа, могут возразить, что загвоздка лишь в недостатке информации и вычислительных ресурсов. Будь у нас полное представление о начальных условиях, мы смогли бы абсолютно точно спрогнозировать результат.

Но реальность совершенно иная: системы настолько сложны, что собрать необходимую информацию невозможно. Видимо, еще важнее другой аспект: такая задача обречена на неудачу даже в теории ввиду вероятностного, а не детерминистического характера реальности, зависящей от мельчайших нюансов.

Именно по этой причине есть резон обсуждать «истинную» вероятность результатов и не позволять себя обманывать детерминистам, у которых либо 0 %, либо 100 %. Что касается спорта, а не подбрасывания монеты, мы по определению не знаем и не можем знать «истинную» вероятность (потому это слово и заключено в кавычки), но целесообразно рассуждать исходя из предположения, будто такая вероятность существует.

Неопределенность второго типа называется гносеологической, или модельной. Она возникает по причине неполного понимания моделируемой ситуации. Гносеологическую неопределенность можно снизить с помощью дополнительных знаний о модели.

Цель количественной оценки неопределенности — уменьшить гносеологическую неопределенность до случайной. На практике границы между ними могут оказаться нечеткими, поскольку системы сложны, а природа реальности вероятностная.

В своей блестящей статье «Toward a theory of everything piece» («На пути к всеобъемлющей теории»), написанной для Pinnacle внештатным автором @PlusEVAnalytics, два упомянутых вида неопределенности описаны соответственно как «технологическая» (случайная) и «параметрическая» (гносеологическая). Надеюсь, нижеследующая цитата прояснит разницу между ними.

«Допустим, вы полагаете, что шансы футбольного клуба на победу составляют 60 %, ставите на него приличные деньги, а клуб проигрывает. Почему вы проиграли? Вполне может быть, что вы правильно оценили шансы, но вам не повезло — произошло событие, вероятность которого составляла 40 %, в итоге вы проиграли. Такова технологическая (случайная) неопределенность — правильная ставка, но не повезло с результатом. Другой вариант. Допустим, ваша оценка оказалась ошибочной — истинная вероятность могла быть 50 %, 30 % или даже 1 %. Вы сделали неплохую, на ваш взгляд, ставку, которая в действительности была никудышной. Такая неопределенность называется параметрической (гносеологической). Поскольку истинная вероятность неизвестна, весьма сложно понять, в какой степени ваши результаты, будь то хорошие или плохие, определяются технологической неопределенностью, а в какой — параметрической».

Моделирование неопределенности в контексте ставок

В среде ставок случайная неопределенность для всех одинакова. Во время спортивных соревнований происходят одни и те же события с одними и теми же влияющими переменными. Реальность для всех игроков одинакова.

Случайную неопределенность достаточно легко моделировать с помощью простого генератора случайных чисел. Рассмотрим соревнование с вероятностью исхода 50 на 50, т. е. коэффициентом 2,00. Для моделирования случайной неопределенности можно просто использовать генератор случайных чисел с выходным диапазоном от 0 до 1. Если число ниже 0,5, ставка выигрышная. Если выше, проигрышная. Распределение результатов (выигрышных и проигрышных ставок) будет в таком случае биномным.

Моделирование гносеологической неопределенности несколько проблематичнее, поскольку не всегда очевидно, каким будет распределение связанных с ней ошибок. @PlusEVAnalytics использует для моделирования бета-распределение, но я не настолько крупный специалист. Мне напрягаться не хочется, ограничусь распределением Гаусса. Я также предположу, что такое распределение гносеологических ошибок вращается вокруг истинной вероятности результата, описанной ниже. Разумеется, при наличии систематических ошибок такое предположение будет неверным.

Как минимум для букмекера это, вероятно, вполне обоснованное предположение, поскольку я уже показывал, что коэффициенты ставок Pinnacle, по крайней мере для крупных спортивных рынков, высокоэффективны. Можно сказать, что в среднем они очень точно отражают базовую истинную вероятность результата, даже если в отдельных случаях бывают ошибки. Верно ли такое же утверждение в отношении игроков? Вероятно, в меньшей степени.

Распределение в гносеологической неопределенности

Чтобы смоделировать последствия гносеологической неопределенности, я создал 1000 гипотетических ставок, в которых истинная вероятность выигрыша для каждой ставки составляет 50 %. Моя гипотетическая модель прогнозирования показала для каждой ставки гносеологическую ошибку в оценке истинной вероятности выигрышей. Размер ошибки определялся шестью различными стандартными отклонениями: 0 %, 1 %, 2 %, 3 %, 4 % и 5 %. Например, для стандартного отклонения 1 % чуть больше двух третей смоделированных «истинных» вероятностей выигрыша составит от 49 % до 51 %, а около 95 % окажется в диапазоне от 48 % до 52 %.

Для более значительных стандартных отклонений распределение «истинных» вероятностей выигрышей, сгенерированных с помощью модели прогнозирования, увеличится, как показано на графике ниже. Очевидно, что при стандартном отклонении 0 % все вероятности выигрыша составят точно 50 %, поэтому данная строка не показана. Чем шире распределение, тем выше гносеологическая неопределенность.

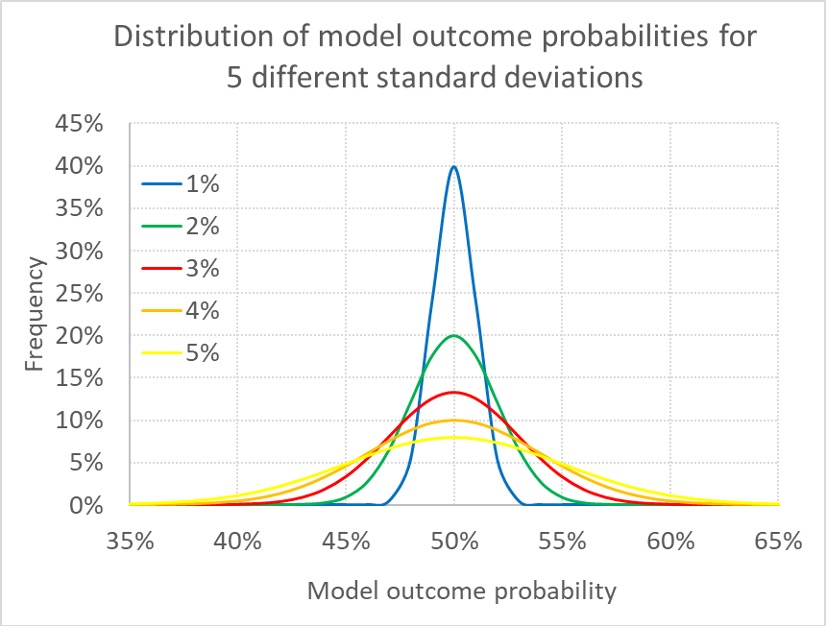
Из графика видно, что хотя каждое распределение вероятности выигрыша представляет эффективную модель — среднее всегда равно 50 %, — размер гносеологической неопределенности меняется.

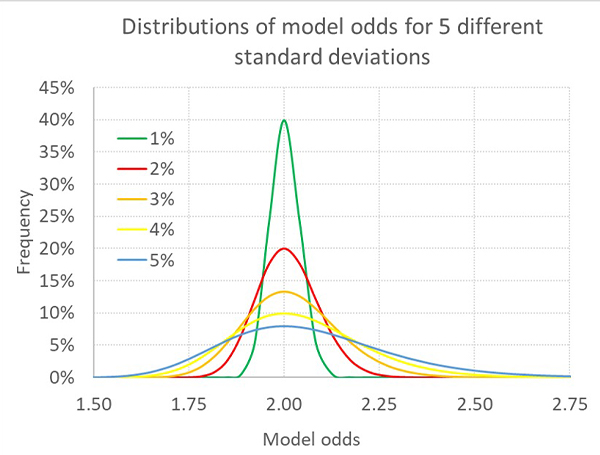
Инвертировав «истинные» вероятности выигрыша, мы получим распределение коэффициентов. Поскольку взаимосвязь между вероятностью выигрыша и предполагаемыми коэффициентами инвертированная, распределение будет логарифмически нормальным.

В примере с 1000 ставок это означает, что смоделированные «истинные» коэффициенты обычно оказываются в диапазонах 1,88–2,13, 1,78–2,28, 1,69–2,46, 1,60–2,66 и 1,52–2,89 для стандартных отклонений 1 %, 2 %, 3 %, 4 % и 5 % соответственно.

Букмекер против игрока

Давайте применим упомянутую модель гносеологической неопределенности к истинным коэффициентам и проведем соревнование между букмекером и игроком. Для каждой ставки букмекер публикует предполагаемые им истинные коэффициенты, уменьшая цену на 2,5 % маржи. Например, если букмекер полагает, что истинная цена 2,00, то публикует 1,95. При 1000 ставок коэффициенты будут меняться в соответствии с показанным выше распределением.

Игрок использует другую модель для оценки истинных коэффициентов. Если коэффициенты, опубликованные букмекером, длиннее, чем оценка игрока, игрок делает ставку на 1 единицу. В противном случае ставки нет.

Для расчета ставок истинные коэффициенты для каждой ставки, неизвестные букмекеру и игроку, составляют 2,00, а результат определяется с помощью генератора случайных чисел. Как уже объяснялось, любое отклонение является здесь следствием случайной неопределенности.

Соревнование повторялось 10 000 раз с моделированием методом Монте-Карло. Посмотрим сначала на среднее число выигравших ставок для каждой из 36 пар «букмекер — игрок» с гносеологической неопределенностью. Чем выше гносеологическая неопределенность (показанная в заголовках строки и столбца) для каждого игрока или букмекера, тем выше вероятность того, что разница между двумя моделями будет выше маржи, поэтому больше шансов на выигрыш ставки.

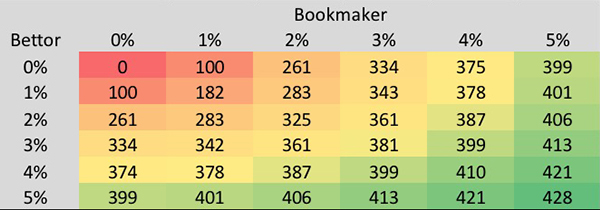
Очевидно, что если букмекер и игрок будут действовать идеально, ни одна из ставок не выиграет, поскольку букмекер всегда будет публиковать 1,95, а игрок всегда будет знать, что это короче истинной цены.

Во второй таблице показан средний (ожидаемый) выигрыш, который удалось получить игроку для каждой пары неопределенностей. Не забывайте, что чем меньше стандартное отклонение, тем ниже гносеологическая неопределенность и тем лучше модель.

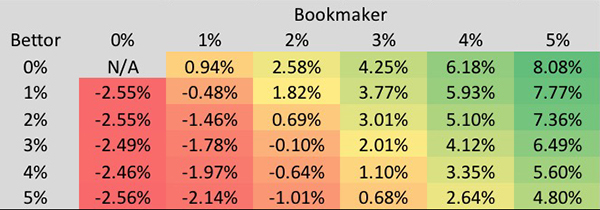
Неудивительно, что если букмекер действует идеально и прогнозирует вероятность для каждой ставки безукоризненно, то как бы ни был хорош игрок, он все равно потеряет деньги в размере маржи (−2,5 %). Незначительные колебания этого значения являются следствием случайной неопределенности. Они уменьшаются по мере увеличения модели по методу Монте-Карло.

Обратите также внимание, что когда модель игрока лучше (неопределенность меньше), чем у букмекера, этого достаточно для генерирования ожидаемой прибыли. Но есть очевидный факт, который приводит в замешательство. Когда модель букмекера плохая, игрок все равно может получить ожидаемую прибыль, даже если его модель хуже. Например, если гносеологическая неопределенность букмекера имеет стандартное отклонение 3 % в вероятности выигрыша, игрок может рассчитывать на +0,68 %, если стандартное отклонение неопределенности в его модели составляет 5 %. Похоже на абсурд.

Асимметрия букмекерства

Чтобы решить этот парадокс, нам нужно выяснить, как задумано соревнование. Как и на любом рынке ставок, букмекер выставляет цену. После этого игрок должен решить, принимает ли он вызов. Он его принимает, только если опубликованные коэффициенты длиннее, чем «истинные» коэффициенты, рассчитанные им самим. Если игрок примет вызов, букмекер не сможет отменить предложение ставки.

Если в моем сценарии модели была гносеологическая неопределенность, 50 % ошибок букмекера означали бы более длинные прогнозируемые «истинные» коэффициенты, чем фактические истинные коэффициенты (2,00), а 50 % — более короткие. Аналогичным образом, 50 % ошибок игрока были бы длиннее или короче 2,00.

Но когда коэффициенты букмекера короче 2,00, меньше вероятность того, что коэффициенты игрока будут еще короче и он решит сделать ставку. Наоборот, вероятность ставки выше, когда коэффициенты букмекера слишком длинные.

Такая асимметрия увеличивает соотношение между ставками с положительными и отрицательными значениями EV. Чем больше гносеологическая неопределенность, тем больше асимметрия. Когда и букмекер, и игрок демонстрируют стандартное отклонение неопределенности 2 %, 56 % ставок имеют положительное значение EV, а средний коэффициент ставок составляет 2,01. Когда стандартное отклонение неопределенности для обоих поднимается до 5 %, 68 % ставок выигрывают при коэффициентах выше 2,00 и среднем значении 2,10.

Если же мы запустим другую модель, в которой и делающий ставку, и принимающий ее должны договориться о принятии ставки при коэффициентах, опубликованных третьим лицом, эта асимметрия в значительной степени уменьшается. В этом случае оба соревнуются также с третьим лицом и его моделью гносеологической неопределенности. Если гносеологическая неопределенность третьего лица невелика, то и делающий ставку, и принимающий ее, если у них одинаковые модели неопределенности, проиграют эквивалент маржи, установленной третьим лицом.

Реальный мир ставок

Все приведенные выводы построены на одном значительном и, вероятно, нереалистичном предположении. Предполагалось, что модели букмекера и игрока полностью независимы друг от друга. В реальности такое маловероятно, поскольку создатели моделей обычно используют одни и те же данные и аналогичные алгоритмы прогнозирования.

Если букмекер зайдет слишком далеко в своей оценке истинных коэффициентов, то, вполне вероятно, игрок тоже так сделает, и наоборот. Некоторые игроки могут отчасти опираться на ставку букмекера.

Любая корреляция между моделями букмекера и игрока снизит значение EV игрока и усложнит выигрыш.

Тем не менее такая модель гносеологической неопределенности играет ключевую роль. С ее помощью можно понять, насколько хорош должен быть типичный букмекер, чтобы сохранить прибыльность, даже при марже в свою пользу. Поскольку букмекеры не могут отменять коэффициенты, уже принятые игроками, они должны быть уверены, что свели гносеологическую неопределенность к минимуму.

Мы никогда не знаем, какие коэффициенты своего рынка букмекер действительно считает «истинными». Не можем мы знать и фактические истинные коэффициенты, полученные в результате таких оценок. Поэтому мы не можем с высокой точностью определить существующую гносеологическую неопределенность.

Поэтому у нас есть все основания предположить, что итоговые коэффициенты букмекера (за вычетом маржи) представляют собой фактические истинные коэффициенты. При этом разница между предытоговыми и итоговыми коэффициентами служит показателем, по которому можно судить о степени ошибочности модели.

Если взять набор завышенных/заниженных предытоговых и итоговых ставок Pinnacle для футбольных матчей английской Премьер-лиги в этом сезоне, вычесть маржу и стандартизировать итоговые коэффициенты до 2,00, стандартное отклонение вероятности победы, вычисленное на основе итоговых ставок, составит чуть более 2 %. Это значение приближается к наименьшим числам в смоделированных мною стандартных отклонениях и еще раз доказывает, что модель Pinnacle весьма эффективно минимизирует гносеологическую неопределенность.

Чтобы победить, игроки должны быть как минимум так же хороши, при асимметрии на их стороне. Если гносеологическая ошибка Pinnacle для матчей с вероятностью победы 50 % составляет всего 2 %, у игрока не так уж много возможностей для улучшения. Разумеется, игроки могут улучшить ситуацию в свою пользу, применяя минимальные пороговые значения EV, прежде чем ставить против Pinnacle. Но любая корреляция моделей усложнит такую задачу.

Мы в очередной раз увидели, что победить букмекера. особенно Pinnacle, весьма непросто. И вот еще одно объяснение. Устанавливая коэффициенты, букмекер, в отличие от своих клиентов, не имеет возможности выбирать, какая ставка будет хорошей. Ему приходится всякий раз рисковать и надеяться, что решение принято правильно. Для Pinnacle игра заключается в минимизации гносеологической неопределенности и максимальном повышении эффективности коэффициентов.

JOSEPH BUCHDAHL