
| Перейти на сайт сейчас |
- Математика распределений значений доходности ставок
- О чем свидетельствует среднеквадратическое отклонение величины дохода?
- Как долго может продлиться карьера неопытных игроков?
Делающие ставки игроки часто чрезмерно поглощены тем, сколько они ставят, на что именно они делают ставки и сколько они могут выиграть (иногда их приоритеты могут быть расставлены в другом порядке). Размер выигрыша по одной ставке имеет большое значение, однако игрокам нужно также учитывать доходность ставок, включенных в выборку более крупных размеров. Как можно смоделировать диапазон возможных значений доходности ставок? Читайте дальше и узнайте ответы на свои вопросы.
В рамках недавнего обсуждения в Твиттере я рассматривал показатели доходности одного известного в Твиттере типстера, специализирующегося на скачках. Прибыль от оборота 1015 рекомендованных этим типстером «ставок дня» одинакового размера (прогнозы по этим ставкам считались наиболее надежными в конкретном временном отрезке) составила –4,3 %.
«Выборка такого размера вполне подходит для проверки общей прибыльности типстера», –
решил я, особенно не задумываясь над этим. В конце концов, тысяча прогнозов – это довольно много, не так ли? Конечно, только в прошлом месяце я снова поднимал вопрос о том, как случайность может влиять на результаты ставок в выборках таких крупных размеров.
Однако разве у нас нет веских оснований считать, что это свидетельствует о том, что надежность прогнозов упомянутого типстера относительно скачек, вероятно, далеко не самая высокая в Интернете, как нас хотят убедить?
Один из моих подписчиков в Твиттере написал мне: «Не то чтобы я не согласен с вашей точкой зрения, но… достаточно ли 1000 ставок для того, чтобы сделать какой-либо точный вывод?».
После минутного размышления я пришел к выводу, что, вероятно, нет. Вот мой ответ.
«Вы действительно правы. Средний коэффициент для выигрышных «ставок дня» – 2,62. Давайте предположим, что коэффициенты (которые не были предоставлены) остальных двух третей ставок, оказавшихся проигрышными, были несколько выше (именно поэтому эти ставки не стали удачными). Таким образом, средний коэффициент составит приблизительно 3,00.
Ожидаемое среднеквадратическое отклонение величины дохода для выборки из 1015 ставок будет равно ориентировочно 0,045 (4,5 %). Предположим, что долгосрочное математическое ожидание для этого типстера составляет –4,5 %. Тогда полученная величина близка к ожидаемому значению. Вместо этого предположим, что математическое ожидание типстера было безубыточным. В этом случае наблюдается одно среднеквадратическое отклонение от ожидаемого значения. В этом нет ничего хорошего, но такая ситуация вполне возможна в условиях естественной вариации.
Теперь давайте предположим, что показатель типстера должен составить +4,5 %. Это соотносится примерно с двумя среднеквадратическими отклонениями от текущего значения или же приблизительным значением вероятности 2,5 %. Типстер может продолжать утверждать, что его долгосрочное математическое ожидание составляло +4,5 % и что ему просто не повезло. Но поскольку ожидаемая доходность по-прежнему должна быть выше, утверждать, что продемонстрированный на примере 1015 ставок результат – всего лишь следствие невезения, становится все сложнее».
Как была получена цифра 4,5 % для ожидаемого среднеквадратического отклонения величины дохода? Цель этой статьи – дать ответ именно на этот вопрос, а также показать, как это знание может помочь во время сравнения фактической эффективности ставок с любыми существующими ожиданиями.
Математика распределений значений доходности ставок
Ставки имеют бинарный характер: они либо выигрывают, либо проигрывают. В ноябре 2018 г. я рассматривал вопрос о том, как биномиальное распределение может использоваться для получения информации о возможном распределении выигрышей и проигрышей применительно к выборке ставок, меняющихся по воле случая. Для выборки ставок в количестве n, где каждая из них имеет «истинную» вероятность выигрыша p, среднеквадратическое отклонение (или разброс) возможных процентных показателей выигрышей определяется по следующей формуле:
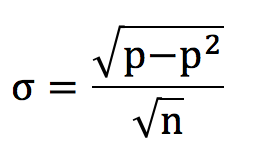
Например, если у нас есть 100 ставок и вероятность выигрыша каждой равна 50 %, можно ожидать, что размер выигрыша составит 50 %, а среднеквадратическое отклонение – 5 %. Другими словами, около двух третей всех возможных результатов будут находиться в пределах от 45 до 55 %, а около 95 % – в диапазоне между 40 и 60 %.
Забудьте о выигрышах и проигрышах. Лучше задумайтесь над тем, как обстоят дела с фактической прибылью. Нам просто нужно немного подкорректировать приведенную выше формулу, включив в нее коэффициенты ставок. Теперь, когда для каждой ставки указан коэффициент o, среднеквадратическое отклонение величин потенциального дохода (или прибыли от оборота) определяется по следующей формуле:
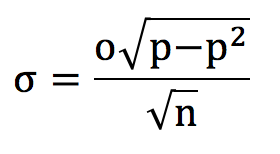
Предположим, что в этом примере «истинная» вероятность выигрыша равна 60 % для предлагаемых букмекером коэффициентов ставок «один к одному», и это действительно очень выгодное предложение. Среднеквадратическое отклонение величин потенциального дохода от 100 ставок составило бы 9,798 %, что сопоставимо с величиной ожидаемого дохода 20 %.
Для «чистых» коэффициентов o = 1 / p. Следовательно, приведенная выше формула приобретает следующий упрощенный вид:
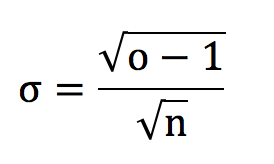
Хотя этот особый случай действительно применим только тогда, когда математическое ожидание игрока является безубыточным (доход = 0 %), разница между o и 1 / p обычно невелика как для неопытных игроков, чьи выигрыши сокращаются из-за букмекерской маржи, так и для опытных игроков, которым удается преодолеть маржу, так что, возможно, для упрощения расчетов имеет смысл использовать этот метод. Это показано на рисунке ниже.
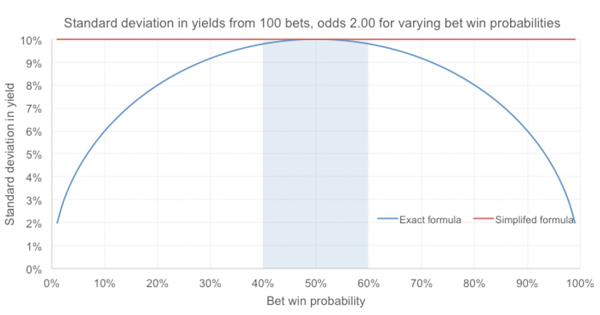
При использовании этой упрощенной формулы в приведенном примере среднеквадратическое отклонение всегда равно 10 % независимо от значения p. Но это значение довольно близко к фактическому среднеквадратическому отклонению для диапазона вероятностей выигрыша от 40 до 60 %. Ни один игрок, по крайней мере это касается игроков Pinnacle, не должен делать ставки «один к одному» при процентном показателе выигрыша 40 % и ниже.
В большинстве случаев размер маржи компании Pinnacle варьируется от 1 до 3 %. Вероятность выигрыша ставки с коэффициентом 2,00 и маржей 2 % составляет приблизительно 49 %. (Фактическое среднеквадратическое отклонение величины дохода от 100 ставок составило бы 9,998 %.) Аналогично процентные показатели выигрышей лучших игроков на ставках мира находятся в диапазоне от 55 до 56 %. (Среднеквадратическое отклонение величины дохода от 100 ставок составило бы 9,928 %.)
О чем свидетельствует среднеквадратическое отклонение величины дохода?
Давайте вернемся к примеру, упомянутому мной в начале, и узнаем, какие выводы можно сделать, обладая информацией о среднеквадратическом отклонении величины дохода. Если представить, что средний коэффициент (o) для 1015 ставок (n) одинакового размера равен 3,00, а «истинная» вероятность выигрыша, подразумеваемая математическим ожиданием –4,3 %, составляет 32 % (p), то применение приведенной выше формулы позволит нам узнать, что среднеквадратическое отклонение величины дохода будет равно 4,39 % (или 4,44 %, если использовать упрощенную формулу).
Распределение величин потенциального дохода от ставок на основании математического ожидания приведено ниже. Вы можете с легкостью построить такое распределение в Excel, просто воспользовавшись функцией NORMDIST. Хотя теоретически эти распределения являются биномиальными и, следовательно, дискретными (если выборка включает более 30 ставок, как в примере выше), нормальное (непрерывное) распределение является очень надежным показателем, который можно применять для приблизительной оценки и который более удобен в использовании при построении таких диаграмм в Excel.
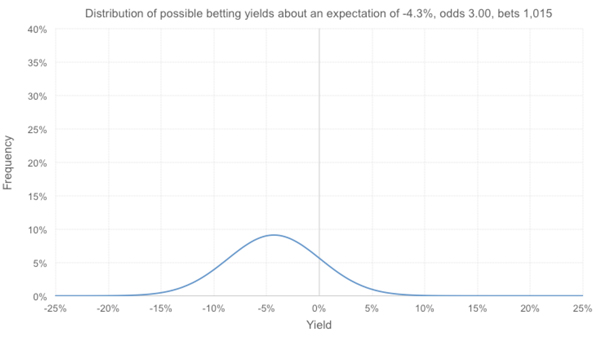
Значения в области ниже кривой синего цвета в сумме составляют 100 %. В этом сценарии мы предположили, что величина фактического дохода соответствует математическому ожиданию. Однако, поскольку коэффициенты достаточно высоки, разброс возможных результатов довольно широк, из чего следует, что наступление даже наиболее вероятного результата (–4,3 %) возможно менее чем в 10 % случаев.
Был ли прав тот подписчик в Твиттере, который засомневался в моем первоначальном наблюдении? В принципе он прав. Хотя прогнозы из изученной сводки результатов типстера нельзя считать примером самых надежных рекомендаций по ставкам на скачки, на основании этого невозможно сделать вывод о том, что деятельность этой консультационной службы характеризуется отрицательным математическим ожиданием. В этом сценарии прибыльность фиксируется в 13,65 % случаев, что находится в пределах статистической приемлемости. Возможно, математическое ожидание этого типстера лучше показателя –4,3 %, и ему просто не повезло.
Вместо этого предположим, что, как упоминалось во вводной части статьи, математическое ожидание типстера является безубыточным. Теперь распределение будет выглядеть следующим образом: в этом сценарии величины потенциального дохода меньше фактических значений в 16,13 % случаев – это значение слишком высоко для того, чтобы исключить вероятность влияния фактора невезения.
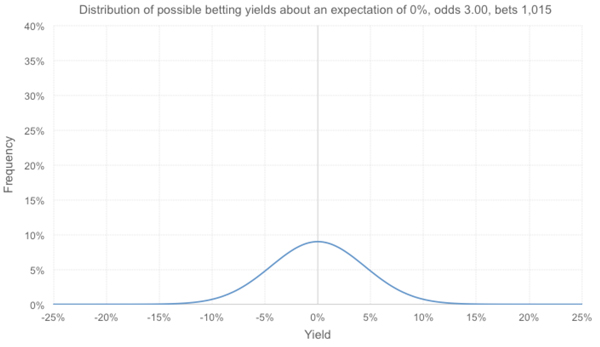 А если математическое ожидание равно +4,3 %? Тогда распределение будет выглядеть следующим образом. В 2,76 % случаев показатели эффективности по-прежнему остаются ниже фактических значений. Цифра небольшая, но можем ли мы полностью исключить влияние невезения? Это относится более чем к одному из 40 типстеров, и подобное может, например, произойти и с 4000 типстеров.
А если математическое ожидание равно +4,3 %? Тогда распределение будет выглядеть следующим образом. В 2,76 % случаев показатели эффективности по-прежнему остаются ниже фактических значений. Цифра небольшая, но можем ли мы полностью исключить влияние невезения? Это относится более чем к одному из 40 типстеров, и подобное может, например, произойти и с 4000 типстеров.
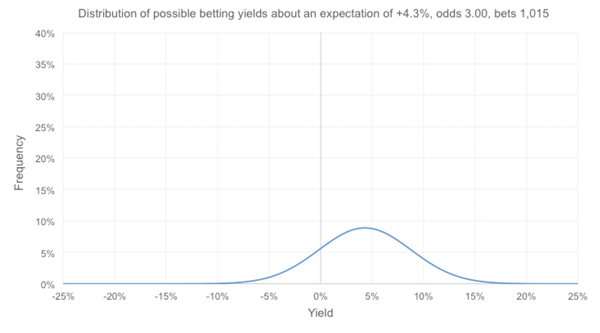
Наконец, давайте предположим, что типстер утверждает, что его прогнозы по ставкам на скачки действительно самые точные в Интернете и что в большинстве случаев эти прогнозы могут обеспечить 10%-ную прибыль от оборота. Далее представлено соответствующее распределение величин потенциального дохода.
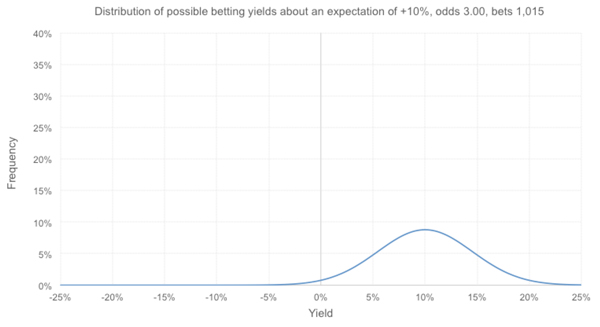
Отсутствие прибыли фиксируется почти в 2 % случаев, а показатель меньше зафиксированного значения 4,3 % наблюдается реже, чем в одном случае из 1000. Возможно, сейчас настало время упрекнуть этого типстера в чрезмерной самоуверенности.
Владея информацией о средней величине коэффициента, размере дохода и количестве ставок, мы можем рассчитать ожидаемое среднеквадратическое отклонение величин потенциального дохода и построить практически любое распределение. Как было показано ранее, фактический достигнутый результат можно противопоставить тому, что мы могли, по нашему мнению, достичь.
Если существует лишь небольшая вероятность получения фактического дохода (и если полагаться на собственное мнение о том, каким должен быть результат, например менее 1 % или ровно 0,1 %), тогда следует рассмотреть возможность проведения оценки математических ожиданий.
Изменение коэффициентов ставок
Как меняется распределение величин потенциального дохода от ставок для разных коэффициентов? Ниже приведены примеры для сценариев с безубыточным математическим ожиданием.
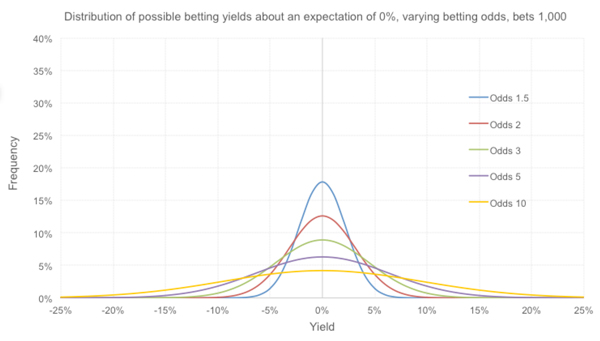
Неудивительно, что чем выше коэффициенты ставок, тем больше дисперсия результатов. Конечно, для этих сценариев с ожидаемой безубыточностью дисперсия (или квадрат среднеквадратического отклонения) прямо пропорциональна значению, полученному в результате вычитания единицы из величины коэффициента.
Если вы делаете ставки с более высокими коэффициентами, вероятность того, что вам удастся превзойти ожидаемые показатели результативности, будет выше в основном благодаря влиянию фактора везения («хвосты» распределений шире, если показатели доходов выше). Конечно, верно и обратное, так как распределения симметричны.
Изменение количества ставок в истории
Мы также можем увидеть, как количество ставок в истории влияет на наше распределение. Из приведенной выше формулы следует, что среднеквадратическое отклонение величины дохода обратно пропорционально квадратному корню из числа ставок. Значит, разброс значений для безубыточного математического ожидания по 100 ставкам одинакового размера (10 %) будет в десять раз больше соответствующего разброса для сводки, включающей 10 000 ставок (1 %). Некоторые другие примеры приведены ниже.
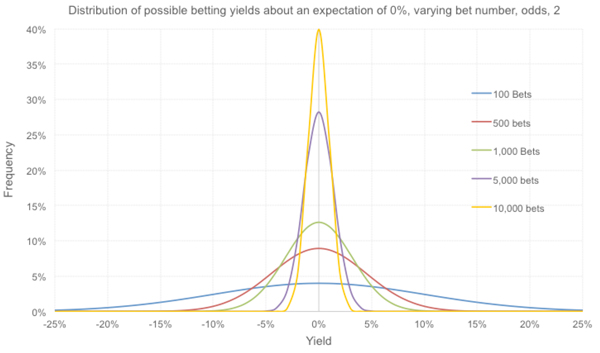
Сужение и увеличение высоты распределений на фоне увеличения количества ставок в истории, по сути, является визуальной интерпретацией закона больших чисел. Чем больше выборка, тем выше вероятность того, что полученный результат является мерой истинного математического ожидания.
Как долго может продлиться карьера неопытных игроков?
В качестве заключительного мысленного эксперимента давайте задумаемся над тем, сколько времени понадобится неопытному игроку Pinnacle с математическим ожиданием –2,5 %, чтобы понять, что ему не хватает навыков. Информация об ожидаемом среднеквадратическом отклонении величины дохода может помочь в поиске ответа на этот вопрос.
В таблице ниже приведены значения вероятности того, что после серии ставок с разными коэффициентами игрок на ставках по-прежнему будет получать прибыль.
В букмекерских конторах, закладывающих небольшую маржу, при определенной доле везения вы сможете многого добиться, особенно если будете делать ставки с высокими коэффициентами. Конечно, если удача отвернется от вас, высокие коэффициенты приведут вас к банкротству гораздо быстрее.
Ниже приведена аналогичная таблица, но на этот раз для вероятностей проигрыша в размере 10 %. Такой результат является просто следствием большей дисперсии (и более широкого диапазона распределений величин потенциального дохода).
Эффективна ли формула, если применить ее к реальным историям ставок?
Вы, возможно, задаетесь вопросом, насколько результативной будет моя формула в случае оценки среднеквадратического отклонения величины дохода от ставок, сделанных с различными коэффициентами. До сих пор я исходил из того, что коэффициенты всех ставок одинаковы. Конечно, большинство игроков делают ставки с разными коэффициентами. Можно ли просто взять среднее значение коэффициентов ставок и получить достоверное среднеквадратическое отклонение величины дохода?
Вернемся к сводке результатов ставок типстера, о котором шла речь в начале этой статьи. Я самостоятельно заполнил недостающие значения коэффициентов (для неопубликованных прогнозов по проигрышным ставкам) и вывел среднее значение, равное 3,00. Мой фактический разброс коэффициентов был значительным: от самых низких значений 8/11 (1,73) до 14/1 (15,0).
Используя генератор случайных чисел в Excel для воспроизведения результатов с математическим ожиданием каждой ставки –4,3 %, я произвел имитационное моделирование по методу Монте-Карло со 100 000 повторений и получил 100 000 различных вариантов величины дохода для выборки из 1015 ставок. Средняя величина дохода составила –4,297 %, а среднеквадратическое отклонение рассчитанных величин было равно 4,373 %. В допустимых пределах погрешности это фактически совпадает со значением 4,389 %, полученным по моей формуле.
Некоторые из вас, возможно, заметили сходство между этой методологией и моим методом на основании t-критерия, используемым для оценки вероятности влияния фактора случайности на характер рассматриваемой сводки результатов ставок. По сути, в основу этих двух методов заложен один и тот же принцип. Более того, даже при небольшом размере выборки (n > 30) биномиальное распределение, нормальное распределение и t-распределение в целом одинаковы.
Надеюсь, что эта статья дала вам более точное представление о различных диапазонах математических ожиданий, которые формируются в сознании игроков в зависимости от их предпочтений и результатов.
Наряду с существующим калькулятором расчета t-критерия, предназначенным для тестирования достоверности сводки результатов ставок, я также разработал калькулятор распределения величин дохода, который вы можете использовать для проверки собственных сводок.
JOSEPH BUCHDAHL
| Перейти на сайт сейчас |

Приобрести смартфон в городе Краснодар ——- Есть интересные моменты, которые могут помочь новичкам! —————————- скачать сайт 1РІРёРЅ